题目内容
如右图,正方形ABCD中,有直径为BC的半圆,BC=2cm,现有E、F两点,分别从B点、A点同时出发,点E沿线段BA以1cm/秒的速度向点A运动,点F沿折线A―D―C以2cm/秒的速度向点C运动,设点E离开B点的时间为t(秒)。

(1)当t为何值时,线段EF与BC平行?
(2)设l<t<2,当t为何值时,EF与半圆相切?
(3)当1≤t<2时,设EF与AC相交于P点,问E、F运动时,点P的位置是否发生变化?若发生变化,请说明理由;若不发生变化,请给予证明,并求AP∶PC的值。
解:(1)设E、F出发后经过t秒时,EF∥BC,

此时BE=t,CF=4-2t,BE=CF,即t=4-2t,∴t=![]()
(2)设E、F出发后t秒时,EF与半圆相切,过F点作FK∥BC,交AB于K。

则BE=t,CF=4-2t,EK=EB-KB=EB-FC=t-(4-2t)=3t-4。
EF=BE+CF(切线长相等)=4-t在Rt△EKF中,EF2=EK2+KF2=(4-t)2=(3t-4)2+22
解得:![]() 或
或![]() (舍去)
(舍去)
(3)当l≤t<2时,P点位置不会发生变化
如图:由![]()
∴AB∥DC,∴△APE∽△CPE
![]() ,即点P的位置与t的数值无关。
,即点P的位置与t的数值无关。
点P的位置不会发生变化,AP∶PC的值为![]()

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 如右图,每个小正方形的边长都是1,△ABC的三个顶点都在格点处,则△ABC的面积是( )
如右图,每个小正方形的边长都是1,△ABC的三个顶点都在格点处,则△ABC的面积是( )| A、4 | B、5 | C、7 | D、8 |
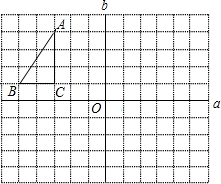 ,请写出△A″B″C″各顶点的坐标,并求出△A″B″C″的周长(结果用根号表示).
,请写出△A″B″C″各顶点的坐标,并求出△A″B″C″的周长(结果用根号表示).

