题目内容
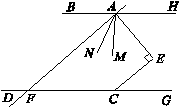
如图，点O在直线AE上，OB平分∠AOC，∠BOD=90°，则∠DOE和∠COB的关系是
- A.互余
- B.互补
- C.相等
- D.和是钝角
A
分析：利用角平分线的性质，可知∠AOB=∠BOC，而∠BOD=90°，可知∠AOB与∠DOE互余，那么∠DOE与∠BOC互余．
解答：∵∠AOB=∠BOC，∠BOC+∠COD=∠BOD=90°，
∴∠AOB+∠DOE=90°，
∴∠DOE+∠COB=90°，故选A．
点评：主要考查了余角和补角的概念与性质．互为余角的两角的和为90°，互为补角的两角之和为180°．解此题的关键是能准确的从题意中找出这两个角之间的数量关系，从而判断出两角之间的关系．
分析：利用角平分线的性质，可知∠AOB=∠BOC，而∠BOD=90°，可知∠AOB与∠DOE互余，那么∠DOE与∠BOC互余．
解答：∵∠AOB=∠BOC，∠BOC+∠COD=∠BOD=90°，
∴∠AOB+∠DOE=90°，
∴∠DOE+∠COB=90°，故选A．
点评：主要考查了余角和补角的概念与性质．互为余角的两角的和为90°，互为补角的两角之和为180°．解此题的关键是能准确的从题意中找出这两个角之间的数量关系，从而判断出两角之间的关系．
练习册系列答案
相关题目
7、如图，点O在直线AE上，OB平分∠AOC，∠BOD=90°，则∠DOE和∠COB的关系是（ ）
.
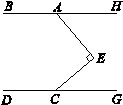
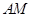平分∠EAF，
平分∠BAE. 试探究∠
，∠AFG的数量关系.
