题目内容
(北师大版)如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为| 2 |
| 2 |
(1)求点A的坐标及∠CAO的度数;
(2)⊙B以每秒1个单位长度的速度沿x轴负方向平移,同时,直线a绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线a也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度;
(3)如图2,过A,O,C三点作⊙O1,点E是劣弧
 |
| AO |
 |
| AO |
| EC-EA |
| EO |


分析:(1)已知点A,C的坐标,故可推出OA=OC,最后可得∠CAO=45°.
(2)依题意,设⊙B平移t秒到⊙B1处与⊙O第一次相切,连接B1O,B1N,则MN=3.连接B1A,B1P可推出∠PAB1=∠NAB1.又因为OA=OB1=
,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠PAC=90°.然后可得直线AC绕点A平均每秒旋转90度.
(3)在CE上截取CK=EA,连接OK,证明△OAE≌△OCK推出OE=OK,∠EOA=∠KOC,∠EOK=∠AOC=90°.最后可证明
=
.
(2)依题意,设⊙B平移t秒到⊙B1处与⊙O第一次相切,连接B1O,B1N,则MN=3.连接B1A,B1P可推出∠PAB1=∠NAB1.又因为OA=OB1=
| 2 |
(3)在CE上截取CK=EA,连接OK,证明△OAE≌△OCK推出OE=OK,∠EOA=∠KOC,∠EOK=∠AOC=90°.最后可证明
| EC-EA |
| EO |
| 2 |
解答: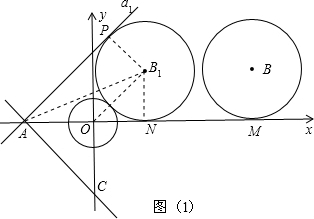 解:(1)令直线a:y=-x-
解:(1)令直线a:y=-x-
中,y=0求出x=-
,
∴A(-
,0),
令x=0求出y=-
,∴C(0,-
),
∴OA=OC,
∵OA⊥OC,
∴△AOC为等腰直角三角形,
∴∠CAO=45°;
(2)如图,设⊙B平移t秒到⊙B1处与⊙O第一次相切,此时,直线α旋转到α1恰好与⊙B1第一次相切于点P,⊙B1与x轴相切于点N,
连接B1O,B1N,则MN=t,OB1=
,
B1N⊥AN,∴MN=3,即t=3.
连接B1A,B1P.则B1P⊥AP,B1P=B1N.∴∠PAB1=∠NAB1
∵OA=OB1=
,∴∠AB1O=∠NAB1∴∠PAB1=∠AB1O.∴PA∥B1O.
在Rt△NOB1中,∠B1ON=45°,
∴∠PAN=45°,∴∠PAC=90°,即顺时针转动270°,
∴直线AC绕点A平均每秒90°.
(3)
的值不变,等于
,如图
在CE上截取CK=EA,连接OK,
∵∠OAE=∠OCK,OA=OC,
∴△OAE≌△OCK,
∴OE=OK,∠EOA=∠KOC,
∴∠EOK=∠AOC=90°,
∴EK=
EO,∴
=
.
 解:(1)令直线a:y=-x-
解:(1)令直线a:y=-x-| 2 |
| 2 |
∴A(-
| 2 |
令x=0求出y=-
| 2 |
| 2 |
∴OA=OC,
∵OA⊥OC,
∴△AOC为等腰直角三角形,
∴∠CAO=45°;
(2)如图,设⊙B平移t秒到⊙B1处与⊙O第一次相切,此时,直线α旋转到α1恰好与⊙B1第一次相切于点P,⊙B1与x轴相切于点N,
连接B1O,B1N,则MN=t,OB1=
| 2 |
B1N⊥AN,∴MN=3,即t=3.
连接B1A,B1P.则B1P⊥AP,B1P=B1N.∴∠PAB1=∠NAB1
∵OA=OB1=
| 2 |

在Rt△NOB1中,∠B1ON=45°,
∴∠PAN=45°,∴∠PAC=90°,即顺时针转动270°,
∴直线AC绕点A平均每秒90°.
(3)
| EC-EA |
| EO |
| 2 |
在CE上截取CK=EA,连接OK,
∵∠OAE=∠OCK,OA=OC,
∴△OAE≌△OCK,
∴OE=OK,∠EOA=∠KOC,
∴∠EOK=∠AOC=90°,
∴EK=
| 2 |
| EC-EA |
| EO |
| 2 |
点评:命题立意:此题综合考查了点的坐标的求法、函数、图形的平移与旋转、圆的有关性质等知识.此题综合性强,难度较大,把重点知识穿插进行了考查.

练习册系列答案
相关题目
(北师大版)如图①,有6张写有汉字的卡片,它们的背面 都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开一张是汉字“自”的概率是( )
都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开一张是汉字“自”的概率是( )
 都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开一张是汉字“自”的概率是( )
都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开一张是汉字“自”的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是
24、(北师大版)如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是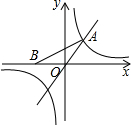 (北师大版)如图,已知点A是一次函数y=x的图象与反比例函数y=
(北师大版)如图,已知点A是一次函数y=x的图象与反比例函数y= 17、(北师大版)如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB.其中相似的为( )
17、(北师大版)如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△CFB.其中相似的为( )