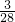Question

现给出1个30°的角，3个45°的角，3个60°的角和1个90°的角从中任取3个角，能构成直角三角形的机会是（　　）

• A、

  9

  56

• B、

  3

  8

• C、

  3

  28

• D、不能确定

Answer 1

分析：因为从各角中取出三个角先取出的角不放回去，所以应考虑到取出直角三角形时的顺序．

解答：解：∵构成直角三角形的情况共两种，第一种可能是：
90、30、60，90、60、30，30、90、60，30、60、90，60、30、90，60、90、30，
当先取出30°的角，再取出60°的角，最后取出90°其概率为

1

8

×

3

7

×

1

6

=

1

112

；
当先取出30°的角，再取出90°的角，最后取出60°其概率为

1

8

×

1

7

×

3

6

=

1

112

；
此六种情况的概率均为

1

112

，
∴此种情况的总概率为

6

112

=

3

56

；
第二种组成三角形的情况为：
90、45、45，45、90、45，45、45、90，
当先取出90°的角，依次取出两个45°的角，其概率为

1

8

×

3

7

×

2

6

=

1

56

，
此三种情况的概率和为

3

56

，
∴能构成直角三角形的机会是

3

56

+

3

56

=

6

56

=

3

28

．
故选C．

点评：本题考查的是概率公式，用到的知识点为：概率等于所求情况数与总情况数之比．