Question

【题目】已知正方形，P为射线上的一点，以为边作正方形，使点F在线段的延长线上，连接.

（1）如图1，若点P在线段的延长线上，判断的形状，并说明理由；

（2）如图2，若点P在线段上

①若点P是线段的中点，判断的形状，并说明理由；

②当时，请直接写出的度数.

Answer 1

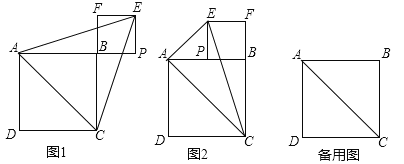
【答案】（1）等腰三角形，见解析；（2）①直角三角形，见解析；②

【解析】

（1）由正方形的性质可得AB=BC，BF=BP，∠ABC=90°=∠EFB=∠EPB，通过证明△AFB≌△CPB，可得AF=CP，∠AFB=∠CPB，由“SAS”可证△AFE≌△CFE，可得AE=CE，即△ACE是等腰三角形；
（2）设AP=PB=PE=EF=BF=a，则AB=2a=BC，CF=3a，由勾股定理的逆定理可证△ACE是直角三角形；
（3）由正方形的性质可得BE=PB=AB，即可求∠EAB=67.5°，即可求∠CAE的度数．

解：（1）△ACE等腰三角形
理由如下：
如图，连接AF，CP，

∵四边形ABCD，四边形FBPE是正方形
∴AB=BC，BF=BP，∠ABC=90°=∠EFB=∠EPB，
∴∠ABF=∠CBP=90°，且AB=BC，BF=BP
∴△AFB≌△CPB（SAS）
∴AF=CP，∠AFB=∠CPB，
∴∠AFB+∠EFB=∠CPB+∠EPB
∴∠AFE=∠CPE，且AF=CP，EF=EP，
∴△AFE≌△CFE（SAS）
∴AE=CE，
∴△ACE是等腰三角形
（2）△ACE是直角三角形
理由如下：
∵点P是线段AB的中点，
∴AP=PB=AB
设AP=PB=PE=EF=BF=a，则AB=2a=BC，CF=3a，
∵AC2=AD2+CD2=8a2，CE2=CF2+EF2=10a2，AE2=AP2+PE2=2a2，
∴CE2=AC2+AE2，
∴△ACE是直角三角形
（3）如图,连接BE，

∵四边形ABCD，四边形FBPE是正方形,
∴∠CAB=∠EBP=45°，BE=PB,
∵AB=PB,
∴AB=BE,
∴∠EAB=∠AEB=67.5°,
∴∠CAE=∠EAB+∠CAB=112.5°.