题目内容
 如图,双曲线y=
如图,双曲线y= (x>0)与矩形OABC的边BC,BA分别交于点E,F,且AF=BF,连接EF,则△OEF的面积为
(x>0)与矩形OABC的边BC,BA分别交于点E,F,且AF=BF,连接EF,则△OEF的面积为
- A.1.5
- B.2
- C.2.5
- D.3
A
分析:设B(a,b),根据题意得F ,由点F在双曲线
,由点F在双曲线 上,得a×
上,得a× =2,即ab=4,E、B两点纵坐标相等,且E点在双曲线
=2,即ab=4,E、B两点纵坐标相等,且E点在双曲线 上,则E(
上,则E( ,b),再根据S△OEF=S梯形OFBC-S△OEC-S△FBE求解.
,b),再根据S△OEF=S梯形OFBC-S△OEC-S△FBE求解.
解答: 解:如图,设点B的坐标为(a,b),则点F的坐标为
解:如图,设点B的坐标为(a,b),则点F的坐标为 .
.
∵点F在双曲线 上,
上,
∴a× =2,
=2,
解得ab=4,
又∵点E在双曲线上,且纵坐标为b,所以点E的坐标为( ,b),则
,b),则
S△OEF=S梯形OFBC-S△OEC-S△FBE,
= ×(
×( +b)a-
+b)a- ×b×
×b× -
- ×
× ×(a-
×(a- )
)
= (ab+1-2)
(ab+1-2)
= .
.
故选:A.
点评:本题考查了反比例函数图象上点的性质,直角坐标系中三角形面积的表示方法.注意双曲线上点的横坐标与纵坐标的积为常数.
分析:设B(a,b),根据题意得F
 ,由点F在双曲线
,由点F在双曲线 上,得a×
上,得a× =2,即ab=4,E、B两点纵坐标相等,且E点在双曲线
=2,即ab=4,E、B两点纵坐标相等,且E点在双曲线 上,则E(
上,则E( ,b),再根据S△OEF=S梯形OFBC-S△OEC-S△FBE求解.
,b),再根据S△OEF=S梯形OFBC-S△OEC-S△FBE求解.解答:
 解:如图,设点B的坐标为(a,b),则点F的坐标为
解:如图,设点B的坐标为(a,b),则点F的坐标为 .
.∵点F在双曲线
 上,
上,∴a×
 =2,
=2,解得ab=4,
又∵点E在双曲线上,且纵坐标为b,所以点E的坐标为(
 ,b),则
,b),则S△OEF=S梯形OFBC-S△OEC-S△FBE,
=
 ×(
×( +b)a-
+b)a- ×b×
×b× -
- ×
× ×(a-
×(a- )
)=
 (ab+1-2)
(ab+1-2)=
 .
.故选:A.
点评:本题考查了反比例函数图象上点的性质,直角坐标系中三角形面积的表示方法.注意双曲线上点的横坐标与纵坐标的积为常数.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
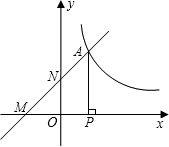 A作AP⊥X轴于点P.
A作AP⊥X轴于点P.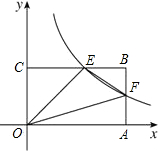 如图,双曲线
如图,双曲线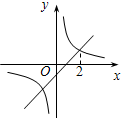 如图,双曲线y1=
如图,双曲线y1=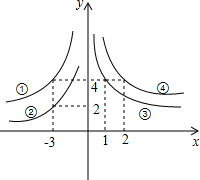 (2013•台州二模)如图,双曲线y=-
(2013•台州二模)如图,双曲线y=-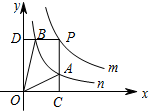 (2012•郑州模拟)如图,双曲线
(2012•郑州模拟)如图,双曲线