题目内容
如图所示,某学校要建一个中间有两道篱笆隔断的长方形花圃,花圃的一边靠墙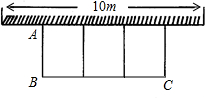 (墙的最大可利用长度为10m),现有篱笆长24m.设花圃的宽AB为xm,面积为Sm2.
(墙的最大可利用长度为10m),现有篱笆长24m.设花圃的宽AB为xm,面积为Sm2.(1)求S与x之间的函数关系式;
(2)如果要围成面积为32m2的花圃,AB的长是多少米?
(3)能围成面积比32m2更大的花圃吗?如果能,请求出最大面积,并给出设计方案;如果不能,请说明理由.
分析:(1)求出S=AB×BC代入即可;
(2)求出方程-4x2+24x=32的解即可;
(3)把解析式化成顶点式,求出顶点的坐标即可得到答案.
(2)求出方程-4x2+24x=32的解即可;
(3)把解析式化成顶点式,求出顶点的坐标即可得到答案.
解答:(1)解:BC=24-4x,
∴S=x(24-4x)=-4x2+24x,
答:S与x之间的函数关系式是S=-4x2+24x.
(2)解:当S=32时,-4x2+24x=32,
解得x1=2,x2=4,
∵墙的最大可利用长度为10m,
∴0<24-4x≤10,
≤x<6,
∴x1=2舍去,x=4,
即花圃的宽AB为4m,
答:如果要围成面积为32m2的花圃,AB的长是4米.
(3)解:∵S=-4x2+24x=-4(x-3)2+36,
∴当x>3时,S随x的增大而减小,
∵
≤x<6,
∴当x=
时,S最大=-4(
-3)2+36=35>32
∴能围成面积比32m2更大的花圃,最大面积为35m2,
方案:∵24-4×
=10,∴花圃的长为10米,宽为3.5米,
答:能围成面积比32m2更大的花圃,最大面积是35m2,方案是花圃的长为10米,宽为3.5米.
∴S=x(24-4x)=-4x2+24x,
答:S与x之间的函数关系式是S=-4x2+24x.
(2)解:当S=32时,-4x2+24x=32,
解得x1=2,x2=4,
∵墙的最大可利用长度为10m,
∴0<24-4x≤10,
| 7 |
| 2 |
∴x1=2舍去,x=4,
即花圃的宽AB为4m,
答:如果要围成面积为32m2的花圃,AB的长是4米.
(3)解:∵S=-4x2+24x=-4(x-3)2+36,
∴当x>3时,S随x的增大而减小,
∵
| 7 |
| 2 |
∴当x=
| 7 |
| 2 |
| 7 |
| 2 |
∴能围成面积比32m2更大的花圃,最大面积为35m2,
方案:∵24-4×
| 7 |
| 2 |
答:能围成面积比32m2更大的花圃,最大面积是35m2,方案是花圃的长为10米,宽为3.5米.
点评:本题主要考查对二次函数的最值,二次函数的解析式,解一元二次方程等知识点的理解和掌握,能把实际问题转化成数学问题是解此题的关键.

练习册系列答案
相关题目
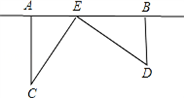
 20、为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
20、为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?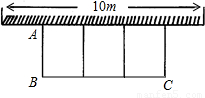
 为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?