题目内容
12. (1)已知一个角是它的余角的一半,求这个角的度数;
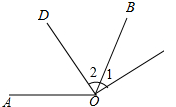
(1)已知一个角是它的余角的一半,求这个角的度数;(2)如图,∠AOB=114°,OD是∠AOB的平分线,∠1与∠2互余,求∠1的度数.
分析 (1)设这个角的度数是x°,则余角是(90-x)°,根据一个角是它的余角的一半即可列方程求解;
(2)首先根据角的平分线的定义求得∠2的度数,然后根据余角的定义求解.
解答 解:(1)设这个角的度数是x°,
根据题意得:x=$\frac{1}{2}$(90-x),
解得:x=30.
则这个角的度数是30°;
(2)∵OD平分∠AOB,
∴∠2=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×114°=57°,
又∵∠1和∠2互余,
∴∠1=90°-∠2=90°-57°=33°.
点评 本题考查了角度的计算,理解角的平分线的定义以及余角的定义是解决本题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
2. 如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
 如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在$\widehat{AB}$上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )| A. | 先变小,后变大 | B. | 先变大,后变小 | ||
| C. | DE与OD的长度保持相等 | D. | 固定不变 |
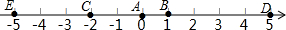 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.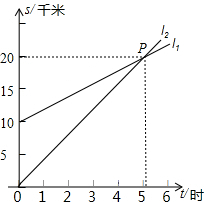 如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:
如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空: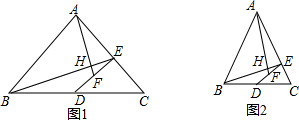
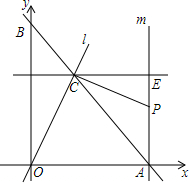 如图,直线y=-x+$\sqrt{2}$分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.
如图,直线y=-x+$\sqrt{2}$分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.