题目内容
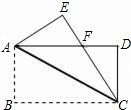
 如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是________平方厘米.
如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是________平方厘米.
48
分析:设这个长方形ABCD的长为a厘米,宽为b厘米.即BC=a,AB=b,则其面积为ab平方厘米,过F作FG⊥CD,FQ⊥BC且分别交CD于G、BC于Q,求出则FQ= b,FG=
b,FG= a,得到△BFC的面积,同理求出△FCD的面积,根据△BDF的面积=△BCD的面积-(△BFC的面积+△CDF的面积),得到6=
a,得到△BFC的面积,同理求出△FCD的面积,根据△BDF的面积=△BCD的面积-(△BFC的面积+△CDF的面积),得到6= ab-(
ab-( ab+
ab+ ab)=
ab)= ab,可求出ab的值,即可得到答案.
ab,可求出ab的值,即可得到答案.
解答: 解:设这个长方形ABCD的长为a厘米,宽为b厘米.即BC=a,AB=b,
解:设这个长方形ABCD的长为a厘米,宽为b厘米.即BC=a,AB=b,
则其面积为ab平方厘米.
∵E为AD的中点,F为CE的中点,
∴过F作FG⊥CD,FQ⊥BC且分别交CD于G、BC于Q,则FQ= CD=
CD= b,FG=
b,FG= a.
a.
∵△BFC的面积= BC•FQ=
BC•FQ= a•
a• b,
b,
同理△FCD的面积= •b•
•b• a,
a,
∴△BDF的面积=△BCD的面积-(△BFC的面积+△CDF的面积),
即:6= ab-(
ab-( ab+
ab+ ab)=
ab)= ab
ab
∴ab=48.
∴长方形ABCD的面积是48平方厘米.
故答案为:48.
点评:本题主要考查了矩形的性质,三角形的中位线,三角形的面积,解一元一次方程等知识点,根据已知求出ab的值是解此题的关键.
分析:设这个长方形ABCD的长为a厘米,宽为b厘米.即BC=a,AB=b,则其面积为ab平方厘米,过F作FG⊥CD,FQ⊥BC且分别交CD于G、BC于Q,求出则FQ=
 b,FG=
b,FG= a,得到△BFC的面积,同理求出△FCD的面积,根据△BDF的面积=△BCD的面积-(△BFC的面积+△CDF的面积),得到6=
a,得到△BFC的面积,同理求出△FCD的面积,根据△BDF的面积=△BCD的面积-(△BFC的面积+△CDF的面积),得到6= ab-(
ab-( ab+
ab+ ab)=
ab)= ab,可求出ab的值,即可得到答案.
ab,可求出ab的值,即可得到答案.解答:
 解:设这个长方形ABCD的长为a厘米,宽为b厘米.即BC=a,AB=b,
解:设这个长方形ABCD的长为a厘米,宽为b厘米.即BC=a,AB=b,则其面积为ab平方厘米.
∵E为AD的中点,F为CE的中点,
∴过F作FG⊥CD,FQ⊥BC且分别交CD于G、BC于Q,则FQ=
 CD=
CD= b,FG=
b,FG= a.
a.∵△BFC的面积=
 BC•FQ=
BC•FQ= a•
a• b,
b,同理△FCD的面积=
 •b•
•b• a,
a,∴△BDF的面积=△BCD的面积-(△BFC的面积+△CDF的面积),
即:6=
 ab-(
ab-( ab+
ab+ ab)=
ab)= ab
ab∴ab=48.
∴长方形ABCD的面积是48平方厘米.
故答案为:48.
点评:本题主要考查了矩形的性质,三角形的中位线,三角形的面积,解一元一次方程等知识点,根据已知求出ab的值是解此题的关键.

练习册系列答案
相关题目
 于点F.
于点F. 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.

