Question

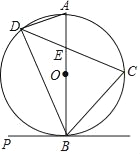
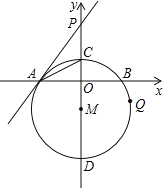
【题目】如图，在直角坐标系中，⊙M的圆心M在y轴上，⊙M与x轴交于点A、B，与y轴交于点C、D，过点A作⊙M的切线AP交y轴于点P，若点C的坐标为（0，2），点A的坐标为（-4，0），

（1）求证：∠PAC＝∠CAO；

（2）求直线PA的解析式；

（3）若点Q为⊙M上任意一点，连接OQ、PQ，问的比值是否发生变化？若不变求出此值；若变化，说明变化规律．

Answer 1

【答案】（1）见解析（2）（3）

【解析】

（1）连接MA，如图1，由PA是⊙M的切线得∠PAC+∠MAC=90°；由MA=MC得∠MCA=∠MAC，又∠OAC+∠MCA=90°，易证∠PAC=∠OAC；

（2）如图1，由于点A的坐标已知，要求直线PA的解析式，只需求出点P的坐标，只需求出OP的长，易证△AOM∽△PAM，根据相似三角形的性质可求出MP，从而可求出OP，问题得以解决；

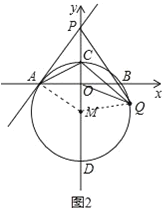
（3）连接MQ，如图2，由于MA=MQ，结合（2）中已证的结论，由此可证到△MOQ∽△MQP，然后运用相似三角形的性质即可解决问题．

（1）连接MA，如图1，

∵PA是⊙M的切线，

∴AM⊥AP，

∴∠PAC+∠MAC=90°，

∵MA=MC，

∴∠MCA=∠MAC，

∵∠OAC+∠MCA=90°，

∴∠PAC=∠OAC；

（2）如图1，

∵∠AMO=∠PMA，∠AOM=∠PAM=90°，

∴△AOM∽△PAM，

∴，

∴MA2=MOMP．

设AM=R，

∵A（-4，0），C（0，2），

∴OA=4,OC=2

在Rt△AOM中，

∵OA=4，OM=R-2，

由AM2=OM2+AO2得，R2=(R-2)2+42

解得，R=5，即AM=5，

∴OM=5-2=3．

∴25=3MP，

∴MP=，

∴OP=MP-OM=-3=，

∴点P的坐标为（0，），

设直线PA的解析式为y=kx+b，

则有，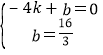

解得，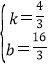

∴直线PA的解析式为y=x+；

（3）连接MQ，如图2，

∵（（2）中已证），MA=MQ，

∴，

∵∠QMO=∠PMQ，

∴△MOQ∽△MQP，

∴，

∴不变，等于．