Question

如图1，AB∥CD，EO和FO交于点O．
（1）试猜想∠1，∠2，∠3的大小关系，并说明理由．
（2）如图2，直线l₁∥l₂，AB⊥l₁，垂足为O，BC与l₂相交于点E，若∠1=30°，则∠B=______．
（3）如图3，AB∥CD，图中∠1，∠2，∠3，…，∠2n-1，∠2n之间有什么关系？（直接写出答案）

Answer 1

解：（1）∠2=∠1+∠3，
理由是：
过O作OM∥AB，
∵AB∥CD，
∴AB∥OM∥CD，
∴∠1=∠NOM，∠3=∠MOP，
∴∠2=∠NOM+∠MOP=∠1+∠3；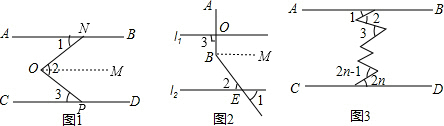

（2）∵AB⊥l₁，
∴∠3=90°，
∵∠1=30°，
∴∠2=∠1=30°，
由（1）知：∠3+∠2=∠ABE，
∴∠ABE=30°+90°=120°，
故答案为：120°；

（3）∠1+∠3+∠5+…+∠2n-1=∠2+∠4+…+∠2n．
分析：（1）过O作OM∥AB，推出AB∥OM∥CD，根据平行线性质得出∠1=∠NOM，∠3=∠MOP，即可求出答案；
（2）求出∠3=90°，∠2=∠1=30°，根据∠3+∠2=∠ABE求出即可；
（3）过各个点作AB的平行线，根据平行线的性质即可得出答案．
点评：本题考查了平行线性质的应用，关键是正确作辅助线，题目比较典型，是一道比较好的题目．