题目内容
等腰△ABC中，AB=AC，延长BA至点D，使得AD=AB，连结CD，则∠BCD=________度．
90
分析：由在△ABC中，AB=AC，AD=AB，即可得AB=AC=AD，然后根据等边对等角与三角形内角和定理，即可求得∠DCB的度数．
解答：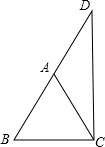
解：∵AB=AC，AD=AB，
∴AB=AC=AD，
∴∠B=∠ACB，∠D=∠ACD，
∵∠B+∠D+∠ACB+∠ACD=180°，
∴∠ACB+∠ACD=90°，
∴∠DCB=90°．
故答案为：90．
点评：此题考查了等腰三角形的性质．此题难度不大，解题的关键是注意数形结合思想的应用．
分析：由在△ABC中，AB=AC，AD=AB，即可得AB=AC=AD，然后根据等边对等角与三角形内角和定理，即可求得∠DCB的度数．
解答：
解：∵AB=AC，AD=AB，∴AB=AC=AD，
∴∠B=∠ACB，∠D=∠ACD，
∵∠B+∠D+∠ACB+∠ACD=180°，
∴∠ACB+∠ACD=90°，
∴∠DCB=90°．
故答案为：90．
点评：此题考查了等腰三角形的性质．此题难度不大，解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
24、等腰△ABC中，AB=AC，D为BC上的一动点，DE∥AC，DF∥AB，分别交AB于E，AC于F，则DE+DF是否随D点变化而变化？请说明理由．
如图，在等腰△ABC中，AB=AC，以AB为直径作⊙O交BC于D，交AC于E，过D点作DF⊥AC于F，有下列结论：
如图，在等腰△ABC中，AB=AC，∠A=50°，边AB的垂直平分线交边AC于点E，则∠EBC=
如图，在等腰△ABC中，AB=AC，O为AB上一点，以O为圆心，OB长为半径的圆交BC于D，DE⊥AC交AC于点E．