Question

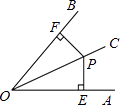
【题目】如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y= （k＞0）的图象与BC边交于点E．

（1）当F为AB的中点时，求该函数的解析式；
（2）当k为何值时，△EFA的面积最大，最大面积是多少？

Answer 1

【答案】
（1）

解：∵在矩形OABC中，OA=3，OC=2，

∴B（3，2），

∵F为AB的中点，

∴F（3，1），

∵点F在反比例函数y= （k＞0）的图象上，

∴k=3，

∴该函数的解析式为y= （x＞0）

（2）

解：由题意知E，F两点坐标分别为E（ ，2），F（3， ），

∴S△EFA= AFBE= × k（3﹣ k），

= k﹣ k2

=﹣ （k2﹣6k+9﹣9）

=﹣ （k﹣3）2+

当k=3时，S有最大值．

S最大值=

【解析】（1）当F为AB的中点时，点F的坐标为（3，1），由此代入求得函数解析式即可；（2）根据图中的点的坐标表示出三角形的面积，得到关于k的二次函数，利用二次函数求出最值即可．