题目内容
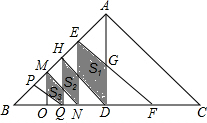 如图,在等腰△ABC中,AD⊥BC,EF∥AC交AD于G,S△AEG=2S△DFG=4,若EF∥HD∥MN∥PQ,AD∥EN∥HQ∥MO,且图中三个阴影四边形的面积分别记为S1,S2,S3,则S2的值为
如图,在等腰△ABC中,AD⊥BC,EF∥AC交AD于G,S△AEG=2S△DFG=4,若EF∥HD∥MN∥PQ,AD∥EN∥HQ∥MO,且图中三个阴影四边形的面积分别记为S1,S2,S3,则S2的值为分析:首先过点E作EK⊥AD于K,过点H作HL⊥EN于L,由在等腰△ABC中,AD⊥BC,EF∥AC,根据等腰三角形的性质,可证得△AEG是等腰三角形,又由S△AEG=2S△DFG=4,易得△EKG≌△FDG,继而求得S1的值,同理可求得S2的值.
解答:解:过点E作EK⊥AD于K,过点H作HL⊥EN于L,
∵在等腰△ABC中,AD⊥BC,
∴∠BAD=∠CAD,
∵EF∥AC,
∴∠EGA=∠CAD,
∴∠EAG=∠EGA,
∴AE=EG,
∴AK=GK,
∴S△AEG=2S△EKG,
∵S△AEG=2S△DFG=4,
∴S△EKG=S△DFG=2,
∵△EKG∽△FDG,
∴△EKG≌△FDG,
∴EK=DF,
∴S1=DN•DG=EK•DG=DF•DG=2S△DFG=4,
∴S△RND=
S1=2,
∵△AEG∽△AHD,AG:AD=2:3,
∴S△AHD:S△AEG=9:4,
∴S△AHD=9,
∴S△EHR=1,
∴S△HLR=
,
∵EF∥HD∥MN∥PQ,AD∥EN∥HQ∥MO,
同理可得:△EHR是等腰三角形,△HLR∽△DNR,
∴S△HLR:S△RND=1:4,
∴HL=
ND,
S2=HL•NR=
ND•DG=S△NDR=2.
故答案为:2.
∵在等腰△ABC中,AD⊥BC,
∴∠BAD=∠CAD,
∵EF∥AC,
∴∠EGA=∠CAD,
∴∠EAG=∠EGA,
∴AE=EG,
∴AK=GK,
∴S△AEG=2S△EKG,
∵S△AEG=2S△DFG=4,
∴S△EKG=S△DFG=2,
∵△EKG∽△FDG,
∴△EKG≌△FDG,

∴EK=DF,
∴S1=DN•DG=EK•DG=DF•DG=2S△DFG=4,
∴S△RND=
| 1 |
| 2 |
∵△AEG∽△AHD,AG:AD=2:3,
∴S△AHD:S△AEG=9:4,
∴S△AHD=9,
∴S△EHR=1,
∴S△HLR=
| 1 |
| 2 |
∵EF∥HD∥MN∥PQ,AD∥EN∥HQ∥MO,
同理可得:△EHR是等腰三角形,△HLR∽△DNR,
∴S△HLR:S△RND=1:4,
∴HL=
| 1 |
| 2 |
S2=HL•NR=
| 1 |
| 2 |
故答案为:2.
点评:此题考查了等腰三角形的性质,相似三角形的判定与性质,以及平行四边形的面积的求解方法等知识.此题综合性较强,难度较大,解题的关键是注意数形结合思想的应用,注意相似三角形的面积的比等于相似比的平方定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
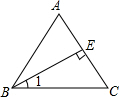 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
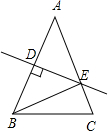 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=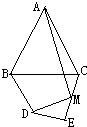 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.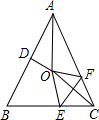 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是