题目内容
已知抛物线y=x2+bx+c(c<0)经过点(c,0),以该抛物线与坐标轴的三个交点为顶点的三角形面积为S,则S可表示为
- A.
 |2+b||b+1|
|2+b||b+1| - B.
 c(1-c)
c(1-c) - C.(b+1)2
- D.

A
分析:把点(c,0)代入抛物线中,可得b、c的关系式,再设抛物线与x轴的交点分别为x1、x2,则x1、x2满足x2+bx+c=0,根据根的判别式结合两点间的距离公式可求|x1-x2|,那么就可得到以该抛物线与坐标轴的三个交点为顶点的三角形面积.
解答:∵抛物线y=x2+bx+c(c<0)经过点(c,0),
∴c2+bc+c=0;
∴c(c+b+1)=0;
∵c<0,
∴c=-b-1;
设x1,x2是一元二次方程x2+bx+c=0的两根,
∴x1+x2=-b,x1•x2=c=-b-1,
∴抛物线与x轴的交点间的距离为|x1-x2|=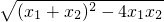 =
= =
= =
= =|2+b|,
=|2+b|,
∴S可表示为 |2+b||b+1|.
|2+b||b+1|.
故选A.
点评:此题考查了点与函数的关系,还考查了二次函数与一元二次方程的关系,要注意根与系数的关系;此题考查了学生的分析能力,属于难度较大的题目.
分析:把点(c,0)代入抛物线中,可得b、c的关系式,再设抛物线与x轴的交点分别为x1、x2,则x1、x2满足x2+bx+c=0,根据根的判别式结合两点间的距离公式可求|x1-x2|,那么就可得到以该抛物线与坐标轴的三个交点为顶点的三角形面积.
解答:∵抛物线y=x2+bx+c(c<0)经过点(c,0),
∴c2+bc+c=0;
∴c(c+b+1)=0;
∵c<0,
∴c=-b-1;
设x1,x2是一元二次方程x2+bx+c=0的两根,
∴x1+x2=-b,x1•x2=c=-b-1,
∴抛物线与x轴的交点间的距离为|x1-x2|=
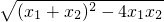 =
= =
= =
= =|2+b|,
=|2+b|,∴S可表示为
 |2+b||b+1|.
|2+b||b+1|.故选A.
点评:此题考查了点与函数的关系,还考查了二次函数与一元二次方程的关系,要注意根与系数的关系;此题考查了学生的分析能力,属于难度较大的题目.

练习册系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.