题目内容
【题目】如图,已知四边形纸片ABCD,现将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线最多有两条,能否做到: (用“能”或“不能”填空).若“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.方法或理由: .
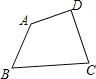
【答案】能;取四边形纸片ABCD各边的中点E、F、G、H,连接EG、FH,则EG、FH为裁剪线,将2绕H旋转180°、4绕G旋转180°,4沿BD方向平移,使B与D重合.
【解析】
试题分析:能做到,方法如下:如图,取四边形纸片ABCD各边的中点E、F、G、H,连接EG、FH,则EG、FH为裁剪线,将2绕H旋转180°、4绕G旋转180°,4沿BD方向平移,是B与D重合,拼成的四边形满足条件.
故答案为:能;如图,取四边形纸片ABCD各边的中点E、F、G、H,连接EG、FH,则EG、FH为裁剪线,将2绕H旋转180°、4绕G旋转180°,4沿BD方向平移,使B与D重合.


【题目】甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在同一次测试中,从两校各随机抽取了30名学生的测试成绩进行调査分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.
甲校 | 54 | 68 | 69 | 76 | 76 | 76 | 76 | 77 | 79 | 82 | 83 | 83 | 84 | 84 | 87 |
87 | 87 | 88 | 88 | 89 | 89 | 89 | 89 | 89 | 90 | 92 | 92 | 92 | 93 | 94 | |
乙校 | 57 | 61 | 63 | 71 | 72 | 73 | 76 | 79 | 80 | 83 | 84 | 84 | 84 | 85 | 85 |
87 | 87 | 88 | 89 | 89 | 90 | 90 | 91 | 92 | 92 | 92 | 92 | 92 | 94 | 94 |
(1)请根据乙校的数据补全条形统计图;

(2)两组样本数据的平均数、中位数、众数如下表所示,请补全表格;
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,请为他们各写出一条可以使用的理由;甲校: ;乙校; .
(4)综合来看,可以推断出 校学生的数学学业水平更好一些,理由为 .
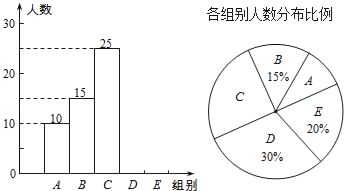
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.