题目内容
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:根据条件可以证得△OCD,△AOD与△AOB都是等边三角形,即可求得圆的半径,再根据阴影部分的面积=扇形AOD的面积-△AOD的面积,据此即可求解.
解答: 解:连接OA,OD.
解:连接OA,OD.
∵AD∥BC,AC平分∠BCD,∠ADC=120°.
∴△OCD是等边三角形.
∴△AOD与△AOB都是等边三角形.
∴AB=OB=OC=CD=AD=2cm
∴△AOD的面积是:
=
cm 2;
扇形AOD的面积是:
=
πcm 2.
阴影部分的面积为:
π-
=(
π-
)cm2,
故选D.
 解:连接OA,OD.
解:连接OA,OD.∵AD∥BC,AC平分∠BCD,∠ADC=120°.
∴△OCD是等边三角形.
∴△AOD与△AOB都是等边三角形.
∴AB=OB=OC=CD=AD=2cm
∴△AOD的面积是:
| ||
| 4 |
| 3 |
扇形AOD的面积是:
| 60π×22 |
| 360 |
| 2 |
| 3 |
阴影部分的面积为:
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
故选D.
点评:本题主要考查了扇形的面积的计算,正确证得△OCD,△AOD与△AOB都是等边三角形是解题的关键.

练习册系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )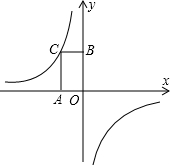 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=