Question

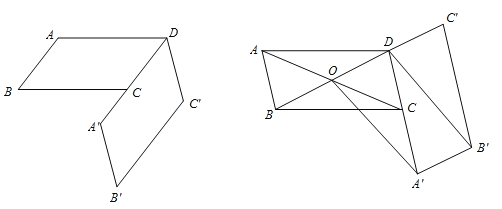
【题目】如图，已知ABCD，AB=m，AD=n，将ABCD绕点D逆时针旋转，得到A’B’CD，点A’在CD延长线上．

（1）若n=4，当B’A’所在直线恰好经过点A时，求点A运动到A’所经过的路径的长度；

（2）连接AC、BD相交于点O，连接OA’、DB’，当四边形OA’B’D为平行四边形时，求的值．

Answer 1

【答案】（1）；（2）

【解析】

（1）连接AA’，依据邻补角、平行线的性质、旋转的性质，得到，；依据等边对等角，得到，从而得到，即可判定是等边三角形，则60°，依据弧长公式计算即可；

（2）由、，依据平行四边形的性质和旋转的性质，得=,,，依据SSS可得≌，依据全等的性质、平行线的性质、等角对等边，得到，即，变式即可.

解：（1）连接AA’，

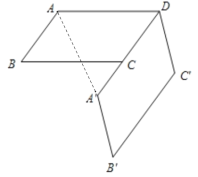
∵ABCD，

∴，

∴，

又由旋转得，，

∴，，

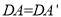∵B’A’所在直线恰好经过点A，

∴，

∴，

又∵，

∴，

∴是等边三角形，

∴60°，

∴点A运动到A’所经过的路径的长度为=；

（2）∵，

∴，，，

∴，

∵将ABCD绕点D逆时针旋转，得到A’B’CD，

∴,,,，

∵，

∴，，

∴,，

∴≌(SSS)，

∴，

∴，

∴，即，

∴．