题目内容
如图，∠ACB=90°，CD⊥AB，垂足为点D．请你猜一猜∠ACD与∠B的关系，并说明理由．
解：∵∠ACB=90°，CD⊥AB，
∴∠ACD+∠BCD=∠ACB=90°，
∠B+∠BCD=180°-90°=90°，
∴∠ACD=∠B．
分析：根据同角的余角相等解答．
点评：本题考查了直角三角形的性质，主要是对同角的余角相等的性质的推导．
∴∠ACD+∠BCD=∠ACB=90°，
∠B+∠BCD=180°-90°=90°，
∴∠ACD=∠B．
分析：根据同角的余角相等解答．
点评：本题考查了直角三角形的性质，主要是对同角的余角相等的性质的推导．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
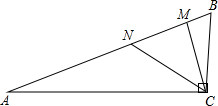如图，∠ACB=90°，AC=12，BC=5，AM=AC，BN=BC，则MN的长是
10、如图，∠ACB=90°，AC=BC，AE⊥CE于E，BD⊥CE于D，AE=5cm，BD=2cm，则DE的长是（ ）
如图，∠ACB=90°，CD⊥AB，垂足为D，下列结论错误的是（ ）
如图，∠ACB=90°，AC=BC，D为AB上一点，AE⊥CD，BF⊥CD，交CD延长线于F点．求证：BF=CE．
如图，∠ACB=90°，AC=AD，DE⊥AB，求证：△CDE是等腰三角形．