题目内容
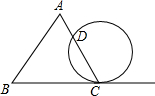 如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则
如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则 | CD |
分析:根据三角形的内角和定理求得∠ACB的度数,再根据弦切角等于它所夹的弧的度数的一半进行求解.
解答:解:∵∠A=70°,∠B=60°,
∴∠ACB=50°,
又圆与直线BC相切于C点,
∴
的度数=2∠ACB=50°×2=100°.
故答案为100°.
∴∠ACB=50°,
又圆与直线BC相切于C点,
∴
 |
| CD |
故答案为100°.
点评:此题考查了三角形的内角和定理以及弦切角定理.
三角形的内角和是180°,弦切角等于它所夹的弧所对的圆周角,圆周角等于它所对的弧所对的圆心角的一半,n°的圆心角对着n°的弧.
三角形的内角和是180°,弦切角等于它所夹的弧所对的圆周角,圆周角等于它所对的弧所对的圆心角的一半,n°的圆心角对着n°的弧.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
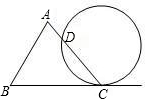 如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则
如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则 |
| CD |
| A、50° | B、60° |
| C、100° | D、120° |
 的度数为何( )
的度数为何( )
 的度数为何( )
的度数为何( )
 的度数为何( )
的度数为何( )