题目内容
如图,直线l:y=| 4 | 3 |
(1)写出点A、B、C的坐标;
(2)若直线l沿x轴正方向平移m(m>0)个单位长度,与BC、AD分别交于E、F点,当四边形ABEF的面积为24时,求直线EF的表达式以及点F到腰CD的距离;
(3)若B点沿BC方向,从B到C运动,速度为每秒1个单位长度,A点同时沿AD方向,从A到D运动,速度为每秒2个单位长度,经过t秒后,A到达P处,
 B到达Q处,问:是否存在t,使得△PQD为直角三角形?若存在,请求出t的值;若不存在,请说明理由.
B到达Q处,问:是否存在t,使得△PQD为直角三角形?若存在,请求出t的值;若不存在,请说明理由.
分析:(1)分别令x=0,y=0求出A、B的坐标.又因为线段BC平行与x轴,易求点C的坐标.
(2)本题有多种证法.证明四边形ABEF为平行四边形求出m的值.设直线EF的解析式为y=
x+b.利用勾股定理以及三角函数值求出有关线段的长.然后利用辅助线的帮助求出点F到腰CD的距离.
(3)本题要依靠辅助线的帮助.过点Q作QK⊥AD于K,根据勾股定理求出PQ,DQ的值.然后分情况讨论t的值.(∠QDP≤∠CDP;∠DPQ=90°;∠PQD=90°)
(2)本题有多种证法.证明四边形ABEF为平行四边形求出m的值.设直线EF的解析式为y=
| 4 |
| 3 |
(3)本题要依靠辅助线的帮助.过点Q作QK⊥AD于K,根据勾股定理求出PQ,DQ的值.然后分情况讨论t的值.(∠QDP≤∠CDP;∠DPQ=90°;∠PQD=90°)
解答:解:(1)令x=0,则y=4;y=0,则x=-3.
∴A(-3,0),B(0,4),C(6,4).
(2)∵BC∥AD,EF∥AB,
∴四边形ABEF为平行四边形.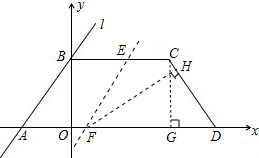
∴SABEF=AF×OB=4m,又SABEF=24,
∴m=6.
∴F(3,0).
设直线EF的表达式为y=
x+b,
则0=
×3+b,b=-4,
∴直线EF的表达式为y=
x-4.
过点C作CG⊥AD于G.
∵四边形ABCD为等腰梯形,
∴DG=OA=3,
在Rt△CGD中,CD=
=
=5sin∠CDG=
=
.
过点F作FH⊥CD于H.
在Rt△FHD中,FD=AD-AF=12-6=6
=sin∠HDF,即
=
,
∴FH=
.
即点F到腰CD的距离为
.
证法二:利用相似可以求得.
过点C作CG⊥AD于G,过点F作FH⊥CD于H.
∵四边形ABCD为等腰梯形,
∴DG=OA=3,
在Rt△CGD中,CD=
=
=5,
在Rt△FHD中,FD=AD-AF=12-6=6.
由Rt△CGD∽Rt△FHD得
=
即
=
,∴FH=
,即点F到腰CD的距离为
.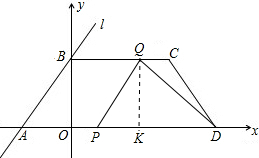
(3)过点Q作QK⊥AD于K,依题意,得
BQ=t,AP=2t,PD=12-t,PK=|t-3|,DK=9-t,0≤t<6.
于是PQ2=42+(t-3)2=t2-6t+25;
DQ2=42+(9-t)2=t2-18t+97PD2=(12-2t)2=4t2-48t+144.
①∵∠QDP≤∠CDP,
∴∠QDP不可能为直角.
②若∠DPQ=90°,则PQ2+PD2=DQ2,t2-6t+25+4t2-48t+144=t2-18t+97.
整理得t2-9t+18=0.
解得t=3或t=6(舍去).
③若∠PQD=90°,则PQ2+DQ2=PD2,t2-6t+25+t2-18t+97=4t2-48t+144.
整理得t2-12t+11=0,解得t=1或t=11(舍去).
综上所述,当t=3或t=1时,△PQD为直角三角形.
∴A(-3,0),B(0,4),C(6,4).
(2)∵BC∥AD,EF∥AB,
∴四边形ABEF为平行四边形.

∴SABEF=AF×OB=4m,又SABEF=24,
∴m=6.
∴F(3,0).
设直线EF的表达式为y=
| 4 |
| 3 |
则0=
| 4 |
| 3 |
∴直线EF的表达式为y=
| 4 |
| 3 |
过点C作CG⊥AD于G.
∵四边形ABCD为等腰梯形,
∴DG=OA=3,
在Rt△CGD中,CD=
| CG2+DG2 |
| 42+32 |
| CG |
| CD |
| 4 |
| 5 |
过点F作FH⊥CD于H.
在Rt△FHD中,FD=AD-AF=12-6=6
| FH |
| FD |
| FH |
| 6 |
| 4 |
| 5 |
∴FH=
| 24 |
| 5 |
即点F到腰CD的距离为
| 24 |
| 5 |
证法二:利用相似可以求得.
过点C作CG⊥AD于G,过点F作FH⊥CD于H.
∵四边形ABCD为等腰梯形,
∴DG=OA=3,
在Rt△CGD中,CD=
| CG2+DG2 |
| 42+32 |
在Rt△FHD中,FD=AD-AF=12-6=6.
由Rt△CGD∽Rt△FHD得
| CG |
| FH |
| CD |
| FD |
即
| 4 |
| FH |
| 5 |
| 6 |
| 24 |
| 5 |
| 24 |
| 5 |

(3)过点Q作QK⊥AD于K,依题意,得
BQ=t,AP=2t,PD=12-t,PK=|t-3|,DK=9-t,0≤t<6.
于是PQ2=42+(t-3)2=t2-6t+25;
DQ2=42+(9-t)2=t2-18t+97PD2=(12-2t)2=4t2-48t+144.
①∵∠QDP≤∠CDP,
∴∠QDP不可能为直角.
②若∠DPQ=90°,则PQ2+PD2=DQ2,t2-6t+25+4t2-48t+144=t2-18t+97.
整理得t2-9t+18=0.
解得t=3或t=6(舍去).
③若∠PQD=90°,则PQ2+DQ2=PD2,t2-6t+25+t2-18t+97=4t2-48t+144.
整理得t2-12t+11=0,解得t=1或t=11(舍去).
综上所述,当t=3或t=1时,△PQD为直角三角形.
点评:本题考查的是分段函数的有关知识,一次函数的综合利用以及勾股定理的应用,难度较大.

练习册系列答案
相关题目

 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( ) 4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )
4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( ) 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数 17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).
17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).