Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ“—÷™£ļ»ÁÕľ£¨‘ŕňńĪŖ–ő![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() īĻ÷Ī∆Ĺ∑÷
īĻ÷Ī∆Ĺ∑÷![]()
![]() .Ķ„
.Ķ„![]() ī”Ķ„
ī”Ķ„![]() ≥Ų∑Ę£¨—ō
≥Ų∑Ę£¨—ō![]() ∑ĹŌÚ‘»ňŔ‘ň∂Į£¨ňŔ∂»ő™
∑ĹŌÚ‘»ňŔ‘ň∂Į£¨ňŔ∂»ő™![]() £ĽÕ¨ Ī£¨Ķ„
£ĽÕ¨ Ī£¨Ķ„![]() ī”Ķ„
ī”Ķ„![]() ≥Ų∑Ę£¨—ō
≥Ų∑Ę£¨—ō![]() ∑ĹŌÚ‘»ňŔ‘ň∂Į£¨ňŔ∂»ő™
∑ĹŌÚ‘»ňŔ‘ň∂Į£¨ňŔ∂»ő™![]() £ĽĶĪ“ĽłŲĶ„Õ£÷Ļ‘ň∂Į£¨ŃŪ“ĽłŲĶ„“≤Õ£÷Ļ‘ň∂Į.ĻżĶ„
£ĽĶĪ“ĽłŲĶ„Õ£÷Ļ‘ň∂Į£¨ŃŪ“ĽłŲĶ„“≤Õ£÷Ļ‘ň∂Į.ĻżĶ„![]() ◊ų
◊ų![]() £¨ĹĽ
£¨ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨ĻżĶ„
£¨ĻżĶ„![]() ◊ų
◊ų![]() £¨∑÷ĪūĹĽ
£¨∑÷ĪūĹĽ![]() £¨
£¨![]() ”ŕĶ„
”ŕĶ„![]() £¨
£¨![]() .ѨŔ
.ѨŔ![]() £¨
£¨![]() .…Ť‘ň∂Į Īľšő™
.…Ť‘ň∂Į Īľšő™![]()
![]() £¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
£¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
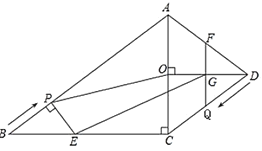
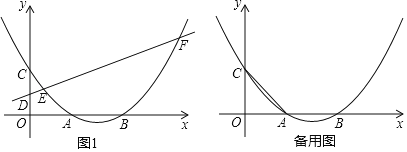
(1)ĶĪ![]() ő™ļő÷Ķ Ī£¨Ķ„
ő™ļő÷Ķ Ī£¨Ķ„![]() ‘ŕ
‘ŕ![]() Ķń∆Ĺ∑÷ŌŖ…Ō£Ņ
Ķń∆Ĺ∑÷ŌŖ…Ō£Ņ
(2)…ŤňńĪŖ–ő![]() Ķń√śĽżő™
Ķń√śĽżő™![]() £¨«ů
£¨«ů![]() ”Ž
”Ž![]() ĶńļĮ żĻōŌĶ Ĺ.
ĶńļĮ żĻōŌĶ Ĺ.
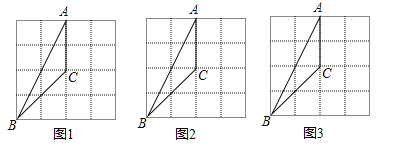
(3)ѨŔ![]() £¨
£¨![]() £¨‘ŕ‘ň∂ĮĻż≥Ő÷–£¨ «∑Ůīś‘ŕń≥“Ľ ĪŅŐ
£¨‘ŕ‘ň∂ĮĻż≥Ő÷–£¨ «∑Ůīś‘ŕń≥“Ľ ĪŅŐ![]() £¨ Ļ
£¨ Ļ![]() £Ņ»Űīś‘ŕ£¨«ů≥Ų
£Ņ»Űīś‘ŕ£¨«ů≥Ų![]() Ķń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
Ķń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
°ĺīūįł°Ņ(1)![]() ő™4√Ž Ī£¨Ķ„
ő™4√Ž Ī£¨Ķ„![]() ‘ŕ
‘ŕ![]() Ķń∆Ĺ∑÷ŌŖ…Ō£Ľ(2)S
Ķń∆Ĺ∑÷ŌŖ…Ō£Ľ(2)S![]()
![]() £Ľ(3)ĶĪ
£Ľ(3)ĶĪ![]() √Ž Ī£¨
√Ž Ī£¨![]() .
.
°ĺĹ‚őŲ°Ņ
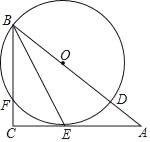
£®1£©łýĺ›ĻīĻ…∂®ņŪ«ůAC£¨łýĺ›![]() ÷§
÷§![]() £¨«ů≥ŲCD°ĘODĶń÷Ķ£¨łýĺ›°ųBPE°◊°ųBACĶ√ĶĹĪ»ņż Ĺ£¨”√ļ¨”–tĶńīķ ż ĹĪŪ ĺ≥ŲPE°ĘBE£¨ĶĪĶ„E‘ŕ°ŌBACĶń∆Ĺ∑÷ŌŖ…Ō Ī£¨“Úő™EP°ÕAB£¨EC°ÕAC£¨Ņ…Ķ√PE=EC£¨”…īňĻĻĹ®∑Ĺ≥ŐľīŅ…Ĺ‚ĺŲő Ő‚£ģ
£¨«ů≥ŲCD°ĘODĶń÷Ķ£¨łýĺ›°ųBPE°◊°ųBACĶ√ĶĹĪ»ņż Ĺ£¨”√ļ¨”–tĶńīķ ż ĹĪŪ ĺ≥ŲPE°ĘBE£¨ĶĪĶ„E‘ŕ°ŌBACĶń∆Ĺ∑÷ŌŖ…Ō Ī£¨“Úő™EP°ÕAB£¨EC°ÕAC£¨Ņ…Ķ√PE=EC£¨”…īňĻĻĹ®∑Ĺ≥ŐľīŅ…Ĺ‚ĺŲő Ő‚£ģ
£®2£©łýĺ›SňńĪŖ–őOPEG=S°ųOEG+S°ųOPE=S°ųOEG+£®S°ųOPC+S°ųPCE-S°ųOEC£©ĻĻĹ®ļĮ żĻōŌĶ ĹľīŅ…£ģ
£®3£©÷§√ų°ŌEOC=°ŌQOG£¨Ņ…Ķ√tan°ŌEOC=tan°ŌQOG£¨Õ∆≥Ų![]() £¨”…īňĻĻĹ®∑Ĺ≥ŐľīŅ…Ĺ‚ĺŲő Ő‚£ģ
£¨”…īňĻĻĹ®∑Ĺ≥ŐľīŅ…Ĺ‚ĺŲő Ő‚£ģ
(1)‘ŕ![]() ÷–£¨°Ŗ
÷–£¨°Ŗ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
°ŗ![]() £¨
£¨
°Ŗ![]() īĻ÷Ī∆Ĺ∑÷ŌŖ∂ő
īĻ÷Ī∆Ĺ∑÷ŌŖ∂ő![]() £¨
£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°Ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°Ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°Ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ°ŌBPE=°ŌBCA=90°„
”÷°ŌB=°ŌB
°ŗ°ųBPE°◊°ųBAC
°ŗ![]()
ľī![]()
°ŗ![]() £¨
£¨![]() £¨
£¨
ĶĪĶ„![]() ‘ŕ
‘ŕ![]() Ķń∆Ĺ∑÷ŌŖ…Ō Ī£¨
Ķń∆Ĺ∑÷ŌŖ…Ō Ī£¨
°Ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() .
.
°ŗĶĪ![]() ő™4√Ž Ī£¨Ķ„
ő™4√Ž Ī£¨Ķ„![]() ‘ŕ
‘ŕ![]() Ķń∆Ĺ∑÷ŌŖ…Ō.
Ķń∆Ĺ∑÷ŌŖ…Ō.
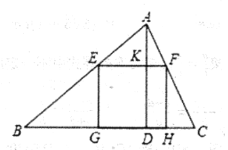
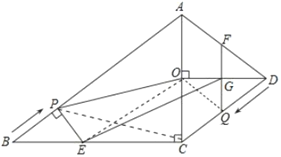
(2)»ÁÕľ£¨Ń¨Ĺ”![]() £¨
£¨![]() .
.
![]()
![]()
![]()
![]() .
.
(3)īś‘ŕ.»ÁÕľ£¨Ń¨Ĺ”![]() .
.
°Ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°Ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ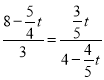 £¨
£¨
’ŻņŪĶ√£ļ![]() £¨
£¨
Ĺ‚Ķ√![]() ĽÚ10(…Š)
ĽÚ10(…Š)
°ŗĶĪ![]() √Ž Ī£¨
√Ž Ī£¨![]() .
.

 ŌįŐ‚ĺę—°ŌĶŃ–īūįł
ŌįŐ‚ĺę—°ŌĶŃ–īūįł