ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏyΘΫ©¹![]() x2©¹
x2©¹![]() x+2
x+2![]() ”κx÷αΫΜ”ΎΒψAΘ§BΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ§Ν§Ϋ”ACΘ°
”κx÷αΫΜ”ΎΒψAΘ§BΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ§Ν§Ϋ”ACΘ°
Θ®1Θ©«σ÷±œΏACΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦ1Θ§ΒψPΈΣ÷±œΏAC…œΖΫ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§ΙΐPΉςPDΓΆABΘ§ΫΜAC”ΎΒψEΘ§ΒψF «œΏΕΈAC…œ“ΜΕ·ΒψΘ§Ν§Ϋ”DFΘ°Β±ΓςPACΒΡΟφΜΐΉν¥σ ±Θ§«σDF+![]() AFΒΡΉν–Γ÷ΒΘΜ
AFΒΡΉν–Γ÷ΒΘΜ
Θ®3Θ©»γΆΦ2Θ§ΫΪΓςOBC»ΤΉ≈ΒψOΥ≥ ±’κ–ΐΉΣ60ΓψΒΟΓςOBΓδCΓδΘ§ΒψG «AC÷–ΒψΘ§ΒψHΈΣ÷±œΏOCΓδ…œ“ΜΕ·ΒψΘ§Β±ΓςGHBΓδΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§÷±Ϋ”–¥≥ωΕ‘”ΠΒΡΒψHΒΡΉχ±ξΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©÷±œΏACΒΡΫβΈω ΫΈΣyΘΫ![]() x+2
x+2![]() ΘΜΘ®2Θ©Ήν–Γ÷Β
ΘΜΘ®2Θ©Ήν–Γ÷Β![]() ΘΜΘ®3Θ©ΒψHΒΡΉχ±ξΈΣΘ®©¹2Θ§©¹
ΘΜΘ®3Θ©ΒψHΒΡΉχ±ξΈΣΘ®©¹2Θ§©¹![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®3
Θ©ΜρΘ®3![]() Θ§
Θ§![]() Θ©ΜρΘ®-3
Θ©ΜρΘ®-3![]() Θ§-
Θ§-![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”…©¹![]() x2©¹
x2©¹![]() x+2
x+2![]() =0Θ§Ζ÷±π«σ≥ωAΘ®©¹6Θ§0Θ©Θ§BΘ®2Θ§0Θ©Θ§‘ΌΝνxΘΫ0Θ§«σ≥ωCΒΡΉχ±ξΘ§…η÷±œΏACΒΡΫβΈω ΫΈΣyΘΫkx+bΘ§ΫΪA,CΒΡΉχ±ξ¥ζ»κΦ¥Ω….
=0Θ§Ζ÷±π«σ≥ωAΘ®©¹6Θ§0Θ©Θ§BΘ®2Θ§0Θ©Θ§‘ΌΝνxΘΫ0Θ§«σ≥ωCΒΡΉχ±ξΘ§…η÷±œΏACΒΡΫβΈω ΫΈΣyΘΫkx+bΘ§ΫΪA,CΒΡΉχ±ξ¥ζ»κΦ¥Ω….
Θ®2Θ©…ηΒψPΘ®tΘ§©¹![]() t2©¹
t2©¹![]() t+2
t+2![]() Θ©Θ§‘ρEΘ®tΘ§
Θ©Θ§‘ρEΘ®tΘ§![]() Θ©Θ§DΘ®tΘ§0Θ©Θ§ΒΟ≥ωPEΘ§‘Όάϊ”Ο»ΐΫ«–ΈΟφΜΐΙΪ ΫΦΤΥψ≥ω»ΐΫ«–ΈPACΘ§ΒΟΒΫΓςPACΒΡΟφΜΐΉν¥σΘ§‘Όάϊ”ΟΙ¥Ι…Ε®άμ«σ≥ωAE, ΉςΒψDΙΊ”Ύ÷±œΏACΒΡΕ‘≥ΤΒψDΓδ
Θ©Θ§DΘ®tΘ§0Θ©Θ§ΒΟ≥ωPEΘ§‘Όάϊ”Ο»ΐΫ«–ΈΟφΜΐΙΪ ΫΦΤΥψ≥ω»ΐΫ«–ΈPACΘ§ΒΟΒΫΓςPACΒΡΟφΜΐΉν¥σΘ§‘Όάϊ”ΟΙ¥Ι…Ε®άμ«σ≥ωAE, ΉςΒψDΙΊ”Ύ÷±œΏACΒΡΕ‘≥ΤΒψDΓδ![]() Θ§ΙΐΒψFΉςFHΓΆx÷αΘ§¥ΙΉψΈΣΒψHΘ§ΙΐΒψDΓδΉςDΓδKΓΆx÷αΘ§¥ΙΉψΈΣΒψKΘ§Ν§Ϋ”DΓδFΘ§ΒΟΒΫ
Θ§ΙΐΒψFΉςFHΓΆx÷αΘ§¥ΙΉψΈΣΒψHΘ§ΙΐΒψDΓδΉςDΓδKΓΆx÷αΘ§¥ΙΉψΈΣΒψKΘ§Ν§Ϋ”DΓδFΘ§ΒΟΒΫ![]() Θ§Φ¥Ω…Ϋβ¥π.
Θ§Φ¥Ω…Ϋβ¥π.
Θ®3Θ©œ»ΗυΨίΧβ“β«σ≥ω![]() Θ§‘Ό≈–Ε®≥ωACΓΈOCΓδΘ§ΒΟΒΫ÷±œΏOCΓδΒΡΫβΈω ΫΈΣyΘΫ
Θ§‘Ό≈–Ε®≥ωACΓΈOCΓδΘ§ΒΟΒΫ÷±œΏOCΓδΒΡΫβΈω ΫΈΣyΘΫ![]() Θ§…ηHΘ®mΘ§
Θ§…ηHΘ®mΘ§![]() Θ©Θ§ΗυΨί–ΐΉΣΒΡ–‘÷ ΒΟΒΫ
Θ©Θ§ΗυΨί–ΐΉΣΒΡ–‘÷ ΒΟΒΫ![]() Θ§Β±ΓςGHBΓδΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§
Θ§Β±ΓςGHBΓδΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§
‘ΌΖ÷»ΐ÷÷«ιΩωΫχ––Χ÷¬έΘ§Φ¥Ω…Ϋβ¥π.
Θ®1Θ©”…©¹![]() x2©¹
x2©¹![]() x+2
x+2![]() =0ΒΟx1ΘΫ©¹6Θ§x2ΘΫ2Θ§
=0ΒΟx1ΘΫ©¹6Θ§x2ΘΫ2Θ§
ΓΏΒψA‘ΎΒψBΒΡΉσ≤ύΘ§
ΓύAΘ®©¹6Θ§0Θ©Θ§BΘ®2Θ§0Θ©Θ§
ΝνxΘΫ0Θ§‘ρyΘΫ2![]() Θ§
Θ§
ΓύCΘ®0Θ§2![]() Θ©Θ§
Θ©Θ§
…η÷±œΏACΒΡΫβΈω ΫΈΣyΘΫkx+bΘ§
‘ρ”–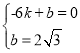 Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ Θ§
Θ§
Γύ÷±œΏACΒΡΫβΈω ΫΈΣyΘΫ![]() ΘΜ
ΘΜ
Θ®2Θ©…ηΒψPΘ®tΘ§©¹![]() t2©¹
t2©¹![]() t+2
t+2![]() Θ©Θ§‘ρEΘ®tΘ§
Θ©Θ§‘ρEΘ®tΘ§![]() Θ©Θ§DΘ®tΘ§0Θ©Θ§
ȩȧDȮtȧ0ȩȧ
ΓύPEΘΫ©¹![]() t2©¹
t2©¹![]() t+2
t+2![]() -(
-(![]() )ΘΫ©¹
)ΘΫ©¹![]() t2©¹
t2©¹![]() tΘ§
tȧ
Γύ![]() Θ§
Θ§
ΓύΒ±tΘΫ©¹3 ±Θ§ΓςPACΒΡΟφΜΐΉν¥σΘ§¥Υ ±PΘ®©¹3Θ§![]() Θ©Θ§EΘ®©¹3Θ§
Θ©Θ§EΘ®©¹3Θ§![]() Θ©Θ§DΘ®©¹3Θ§0Θ©Θ§
Θ©Θ§DΘ®©¹3Θ§0Θ©Θ§
ΓύADΘΫ©¹3©¹Θ®©¹6Θ©ΘΫ3Θ§EDΘΫ![]() Θ§
Θ§
‘ΎRtΓςADE÷–Θ§AEΘΫ![]() Θ§
Θ§
ΓύEDΘΫ![]() Θ§
Θ§
ΓύΓœEADΘΫ30ΓψΘ§
»γΆΦΘ§ΉςΒψDΙΊ”Ύ÷±œΏACΒΡΕ‘≥ΤΒψDΓδ![]() Θ§ΙΐΒψFΉςFHΓΆx÷αΘ§
Θ§ΙΐΒψFΉςFHΓΆx÷αΘ§
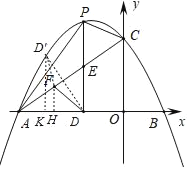
¥ΙΉψΈΣΒψHΘ§ΙΐΒψDΓδΉςDΓδKΓΆx÷αΘ§¥ΙΉψΈΣΒψKΘ§Ν§Ϋ”DΓδFΘ§
‘ΎRtΓςAFH÷–Θ§FHΘΫ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Β±DΓδΘ§FΘ§H»ΐΒψΙ≤œΏ«“”κDΓδK÷ΊΚœ ±Θ§DΓδF+FH»ΓΒΟΉν–Γ÷Β![]() Θ°
Θ°
Θ®3Θ©ΓΏAΘ®©¹6Θ§0Θ©Θ§CΘ®0Θ§2![]() Θ©Θ§ΒψG «AC÷–ΒψΘ§
Θ©Θ§ΒψG «AC÷–ΒψΘ§
Γύ![]() Θ§ΓœAOCΘΫ60ΓψΘ§
Θ§ΓœAOCΘΫ60ΓψΘ§
”…Χβ“βΒΟΓœCOCΓδΘΫ60ΓψΘ§
ΓύACΓΈOCΓδΘ§
Γύ÷±œΏOCΓδΒΡΫβΈω ΫΈΣyΘΫ![]() Θ§
Θ§
…ηHΘ®mΘ§![]() Θ©Θ§
Θ©Θ§
ΓΏΓœBOBΓδΘΫ60ΓψΘ§BΘ®2Θ§0Θ©Θ§
Γύ![]() Θ§
Θ§
Β±ΓςGHBΓδΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§
ΔΌ»τGHΘΫGBΓδΘ§![]() Θ§
Θ§
’ϊάμΒΟΘΚm2+3m©¹12ΘΫ0Θ§
ΫβΒΟΘΚmΘΫ![]() Θ§
Θ§
ΓύH1![]() ΘΜ
ΘΜ
ΔΎ»τHBΓδΘΫGHΘ§![]() Θ§
Θ§
ΫβΒΟmΘΫ©¹2Θ§
Γύ![]() Θ§
Θ§
Δέ»τHBΓδΘΫGBΓδΘ§![]() Θ§
Θ§
’ϊάμΒΟm2ΘΫ18Θ§
ΫβΒΟm=Γά3![]() Θ§
Θ§
ΓύH4Θ®3![]() Θ§
Θ§![]() Θ©Θ§H5Θ®-3
Θ©Θ§H5Θ®-3![]() Θ§-
Θ§-![]() Θ©Θ§
Θ©Θ§
ΉέΚœ“‘…œΩ…ΒΟΒψHΒΡΉχ±ξΈΣΘ®©¹2Θ§©¹![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®3
Θ©ΜρΘ®3![]() Θ§
Θ§![]() Θ©ΜρΘ®-3
Θ©ΜρΘ®-3![]() Θ§-
Θ§-![]() Θ©Θ°
Θ©Θ°

 ΩΎΥψΧβΩ®Φ””Π”ΟΧβΦ·―ΒœΒΝ–¥πΑΗ
ΩΎΥψΧβΩ®Φ””Π”ΟΧβΦ·―ΒœΒΝ–¥πΑΗ ΉέΚœΉ‘≤βœΒΝ–¥πΑΗ
ΉέΚœΉ‘≤βœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΈΣΦφΙΥΦΨΫΎ–‘”ΟΥ°≤ν“λΘ§¥σΝΠΆΤΫχΥ°Ή ‘¥ΫΎ‘ΦΘ§¥”2019Ρξ1‘¬1»’ΤπΘ§Ήώ“ε –÷––Ρ≥««χΨ”Οώ…ζΜν”ΟΥ°ΒΡΫΉΧίΥ°ΝΩΘ§ΫΪ¥”ΓΑ‘¬ΦΤΝΩΓ±Ϋ…Ζ―Βς’ϊΈΣΓΑΡξΦΤΝΩΓ±Ϋ…Ζ―Α¥ΓΑ“ΜΜß“Μ±μΓ±Θ§Ψ”ΟώΦ“ΆΞΈΣ3ΩΎ»ΥΦΤΥψΘ§ΫΉΧί”ΟΥ°ΝΩΦΑΥ°ΦέΦϊœ¬±μΘΚ
Ρξ”ΟΥ°ΝΩΘ®Ε÷Θ© | Υ°ΦέΘ®‘Σ/Ε÷Θ© | |
ΒΎ“ΜΫΉΧί | 0ΓΪ216Θ®Κ§216Θ© |
|
ΒΎΕΰΫΉΧί | 216ΓΪ288Θ®Κ§288Θ© |
|
ΒΎ»ΐΫΉΧί | 288“‘…œ | 8.4 |
–ΓΟςΦ“ΚΆ–ΓΗ’Φ“ΨυΈΣ3ΩΎ÷°Φ“Θ§2018Ρξ»ΪΡξ”ΟΥ°ΝΩΖ÷±πΈΣ260Ε÷ΚΆ300Ε÷Θ§»τΑ¥ΓΑΡξΦΤΝΩΓ±Ϋ…Ζ―±ξΉΦΦΤΥψΘ§–ΓΟςΦ“ΚΆ–ΓΗ’Φ“»ΪΡξ”ΠΫ…Υ°Ζ―Ζ÷±πΈΣ789.6‘ΣΚΆ1008‘Σ.
Θ®1Θ©«σ±μ÷–![]() Θ§
Θ§![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©–ΓΗ’Φ“ Β ©ΫΎΥ°ΦΤΜ°Θ§“‘2018Ρξ”ΟΥ°ΝΩΈΣΤπΒψΘ§‘ΛΦΤ2020Ρξ”ΟΥ°ΝΩΫΒΒΫ243Ε÷Θ§«“¥”2018ΡξΒΫ2020ΡξΟΩΡξ”ΟΥ°ΝΩΒΡΤΫΨυœ¬ΫΒ¬ ΕΦœύΆ§Θ§«κΑ¥¥Υœ¬ΫΒ¬ ΦΤΥψ2021Ρξ–ΓΗ’Φ“”ΟΥ°ΝΩ.
ΓΨΧβΡΩΓΩΡ≥±ΘΫΓΤΖ≥ßΟΩΧλ…ζ≤ζAΘ§BΝΫ÷÷ΤΖ≈ΤΒΡ±ΘΫΓΤΖΙ≤600ΤΩΘ§AΘ§BΝΫ÷÷≤ζΤΖΟΩΤΩΒΡ≥…±ΨΚΆ έΦέ»γœ¬±μΘ§…ηΟΩΧλ…ζ≤ζA≤ζΤΖxΤΩΘ§…ζ≤ζ’βΝΫ÷÷≤ζΤΖΟΩΧλΙ≤Μώάϊy‘ΣΘ°
A | ΓΓB | |
≥…±ΨΘ®‘ΣΘ©/ΤΩ | 50 | ΓΓ35 |
έΦέΘ®‘ΣΘ©/ΤΩ | 70 | ΓΓΓΓΓΓ50 |
Θ®1Θ©«κ«σ≥ωyΙΊ”ΎxΒΡΚ· ΐΙΊœΒΘΜ
Θ®2Θ©ΗΟ≥ßΟΩΧλ…ζ≤ζΒΡAΘ§BΝΫ÷÷≤ζΤΖ±ΜΡ≥Ψ≠œζ…Χ»Ϊ≤ΩΕ©ΙΚΘ§≥ßΦ“Ε‘B≤ζΤΖ≤Μ±δΘ§Ε‘A≤ζΤΖΫχ––»ΟάϊΘ§ΟΩΤΩάϊ»σΫΒΒΆ![]() ‘ΣΘ§≥ßΦ“»γΚΈ…ζ≤ζΩ… ΙΟΩΧλΜώάϊΉν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
‘ΣΘ§≥ßΦ“»γΚΈ…ζ≤ζΩ… ΙΟΩΧλΜώάϊΉν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ