题目内容

已知边长为6的等边三角形ABC，两顶点A、B分别在直角墙面上滑动，连接OC，则OC的长的最大值是________．

$\text{[math]}$
分析：取AB中点D，连接OC、OD、DC，求出AD，根据勾股定理求出DC，根据直角三角形斜边上中线性质求出OD，根据三角形三边关系定理得出OD+DC＞OC，得出当O、D、C三点共线时OC最长，即可得出答案．
解答：

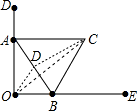
取AB中点D，连接OC、OD、DC，
∵△ABC是等边三角形，
∴AC=BC=AB=6，
∴AD=BD= $\text{[math]}$ AB=3，CD⊥AB，
由勾股定理得：CD= $\text{[math]}$ =3 $\text{[math]}$ ，
∵∠AOB=90°，D为AB中点，
∴OD= $\text{[math]}$ AB=3，
在△DOC中，OD+DC＞OC，
当O、D、C三点共线时OC最长，
最大值是3+3 $\text{[math]}$ ，
故答案为：3+3 $\text{[math]}$ ．
点评：本题考查了等边三角形性质，三角形的三边关系定理，直角三角形斜边上中线性质，勾股定理等知识点的综合运用，题目比较好．

练习册系列答案

练习册吉林教育出版集团有限责任公司系列答案

练习册湖北教育出版社系列答案

相关题目

（2013•黑龙江）已知等边三角形ABC的边长是2，以BC边上的高AB₁为边作等边三角形，得到第一个等边三角形AB₁C₁，再以等边三角形AB₁C₁的B₁C₁边上的高AB₂为边作等边三角形，得到第二个等边三角形AB₂C₂，再以等边三角形AB₂C₂的边B₂C₂边上的高AB₃为边作等边三角形，得到第三个等边AB₃C₃；…，如此下去，这样得到的第n个等边三角形AB_nC_n的面积为

（

）ⁿ

（

）ⁿ

．

（2012•南湖区二模）在特殊四边形的复习课上，王老师出了这样一道题：
如图1，在?ABCD中，E、F、G、H分别为AB，BC，CD，DA边上的动点，连接EG，HF相交于点O，且∠HOE=∠ADC，若AB=a，AD=b，试探究：EG与FH的数量关系．
经过小组讨论后，小聪建议分以下三步进行，请你解答：
（1）特殊情况，探索结论
当?ABCD是边长为a的正方形时（如图2），请写出EG与FH的数量关系（不必证明）；
（2）尝试变题，再探思路
当?ABCD是边长为a的菱形时（如图3），EG与FH又有怎样的数量关系呢？
小聪想：要求EG与FH的数量关系，就要构成全等三角形或相似三角形，于是，分别过点G、H作GM⊥AB于点M，HN⊥BC于点N，在△HNF和△GME中，有∠GME=∠HNF=Rt∠，由菱形面积与性质可得GM=HN，能否从已知条件得到∠MGE=∠NHF呢？请你根据小聪的思路完成解答过程；
（3）特例启发，解答题目
猜想：原题中EG与FH的数量关系是

，并说明理由．

已知等边三角形ABC的边长是2，以BC边上的高AB₁为边作等边三角形，得到第一个等边三角形AB₁C₁，再以等边三角形AB₁C₁的B₁C₁边上的高AB₂为边作等边三角形，得到第二个等边三角形AB₂C₂，再以等边三角形AB₂C₂的边B₂C₂边上的高AB₃为边作等边三角形，得到第三个等边AB₃C₃；…，如此下去，这样得到的第n个等边三角形AB_nC_n的面积为　　．

（2009•河西区一模）如图一，已知点P是边长为a的等边△ABC内任意一点，点P到三边的距离PD、PE、PF的长分别记为h₁，h₂，h₃，则h₁，h₂，h₃之间有什么关系呢？
分析：连接PA、PB、PC，则△ABC被分割成三个三角形，根据：
S_△PAB+S_△PBC+S_△PAC=S_△ABC，即：

，可得

．
问题1：若点P是边长为a的等边△ABC外一点（如图二所示位置），点P到三边的距离PD、PE、PF的长分别记为h₁，h₂，h₃．探索h₁，h₂，h₃之间有什么关系呢？并证明你的结论；
问题2：如图三，正方形ABCD的边长为a，点P是BC边上任意一点（可与B、C重合），B、C、D三点到射线AP的距离分别是h₁，h₂，h₃，设h₁+h₂+h₃=y，线段AP=x，求y与x的函数关系式，并求y的最大值与最小值．

已知边长为6的等边三角形ABC，两顶点A、B分别在直角墙面上滑动，连接OC，则OC的长的最大值是________．

试题分类