Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ![]() ÷–£¨
÷–£¨ ![]() £¨Ķ„
£¨Ķ„![]() ∑÷Īū‘ŕĪŖ
∑÷Īū‘ŕĪŖ![]() …Ō£®Ķ„
…Ō£®Ķ„![]() ≤Ľ”ŽĶ„
≤Ľ”ŽĶ„![]() £¨Ķ„
£¨Ķ„![]() ÷ōļŌ£©£¨
÷ōļŌ£©£¨![]() £¨Ĺę
£¨Ĺę![]() »∆Ķ„
»∆Ķ„![]() ň≥ Ī’Ž–ż◊™Ķ√ĶĹ
ň≥ Ī’Ž–ż◊™Ķ√ĶĹ![]() £ģ
£ģ
£®1£©ĶĪĶ„![]() ‘ŕ
‘ŕ![]() …Ō Ī£¨Ń¨Ĺ”
…Ō Ī£¨Ń¨Ĺ”![]() £¨
£¨
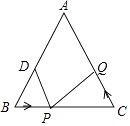
ĘŔ»ÁÕľ1£¨ ![]() £¨ŌŖ∂ő
£¨ŌŖ∂ő![]() ĶńőĽ÷√ĻōŌĶ «_____________£Ľ
ĶńőĽ÷√ĻōŌĶ «_____________£Ľ
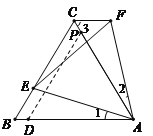
Ęŕ»ÁÕľ2£¨ ![]() £¨īň Ī
£¨īň Ī![]() ĽĻ¬ķ◊„ĘŔ÷–ĶńőĽ÷√ĻōŌĶ¬ū£Ņ»Ű¬ķ◊„£¨«Ž÷§√ųń„ĶńĹŠ¬Ř£Ľ»Ű≤Ľ¬ķ◊„£¨«ŽňĶ√ųņŪ”…£ģ
ĽĻ¬ķ◊„ĘŔ÷–ĶńőĽ÷√ĻōŌĶ¬ū£Ņ»Ű¬ķ◊„£¨«Ž÷§√ųń„ĶńĹŠ¬Ř£Ľ»Ű≤Ľ¬ķ◊„£¨«ŽňĶ√ųņŪ”…£ģ
£®2£©»Ű![]() £¨‘ŕ
£¨‘ŕ![]() »∆Ķ„
»∆Ķ„![]() ň≥ Ī’Ž–ż◊™Ļż≥Ő÷–£¨Ķ„
ň≥ Ī’Ž–ż◊™Ļż≥Ő÷–£¨Ķ„![]() Ķŕ“Ľīő¬š‘ŕ…šŌŖ
Ķŕ“Ľīő¬š‘ŕ…šŌŖ![]() …Ō Ī£¨Ń¨Ĺ”
…Ō Ī£¨Ń¨Ĺ”![]() £¨īň Ī
£¨īň Ī![]() ĽĻ¬ķ◊„£®1£©ĘŔ÷–ĶńőĽ÷√ĻōŌĶ¬ū£Ņ»Ű¬ķ◊„£¨«Ž÷§√ųń„ĶńĹŠ¬Ř£¨≤Ę÷ĪĹ”–ī≥Ų
ĽĻ¬ķ◊„£®1£©ĘŔ÷–ĶńőĽ÷√ĻōŌĶ¬ū£Ņ»Ű¬ķ◊„£¨«Ž÷§√ųń„ĶńĹŠ¬Ř£¨≤Ę÷ĪĹ”–ī≥Ų![]() Ķń»°÷Ķ∑∂őߣ®”√ļ¨
Ķń»°÷Ķ∑∂őߣ®”√ļ¨![]() Ķń Ĺ◊”ĪŪ ĺ£©£Ľ»Ű≤Ľ¬ķ◊„£¨«ŽňĶ√ųņŪ”…£ģ
Ķń Ĺ◊”ĪŪ ĺ£©£Ľ»Ű≤Ľ¬ķ◊„£¨«ŽňĶ√ųņŪ”…£ģ

°ĺīūįł°Ņ£®1£©ĘŔ∆Ĺ––![]() £¨Ęŕ¬ķ◊„£®ĽÚ
£¨Ęŕ¬ķ◊„£®ĽÚ![]() £©£¨ņŪ”…ľŻĹ‚őŲ£Ľ
£©£¨ņŪ”…ľŻĹ‚őŲ£Ľ
£®2£©¬ķ◊„£®ĽÚ![]() £©£¨
£©£¨
ĶĪ![]() Ī£¨
Ī£¨ ![]() £Ľ
£Ľ
ĶĪ![]() Ī£¨
Ī£¨ ![]()
£®ĽÚ![]() £©
£©
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©ĘŔ”…![]() °◊
°◊![]() ,
, ![]() £¨
£¨ ![]() °’
°’![]() ,”…īň
,”…īň![]() °◊
°◊![]() ”…
”…![]() =
=![]() ,Ņ…Ķ√
,Ņ…Ķ√![]() .
.
Ęŕ”…![]() £¨
£¨ ![]() Ķ√
Ķ√![]() «Ķ»ĪŖ»żĹ«–ő£¨”…
«Ķ»ĪŖ»żĹ«–ő£¨”…![]() «Ķ»ĪŖ»żĹ«–ő£¨
«Ķ»ĪŖ»żĹ«–ő£¨ ![]() £¨”…ĪŖĹ«ĪŖŅ…÷§
£¨”…ĪŖĹ«ĪŖŅ…÷§![]() °’
°’![]() £¨”…»ęĶ»»żĹ«–ő∂‘”¶Ĺ«ŌŗĶ»£¨”÷ «ńŕīŪĹ«£¨Ņ…÷§
£¨”…»ęĶ»»żĹ«–ő∂‘”¶Ĺ«ŌŗĶ»£¨”÷ «ńŕīŪĹ«£¨Ņ…÷§![]() £Ľ
£Ľ
£®2£©![]() £ļ
£ļ ![]() Ī£¨”…
Ī£¨”…![]() Ķ√
Ķ√![]() °◊
°◊![]() £¨”…
£¨”…![]()
Ķ√![]() °◊
°◊![]() £¨ĹÝ∂Ý
£¨ĹÝ∂Ý![]() £¨ĶĪ
£¨ĶĪ![]() £¨Õ¨ņŪŅ…÷§
£¨Õ¨ņŪŅ…÷§![]() .
.
‘Ő‚Ĺ‚őŲ£ļ£®1£©ĘŔ∆Ĺ––![]()
ņŪ”…£ļ°Ŗ![]() £¨
£¨ ![]() £¨
£¨
°ŗ![]()
![]() £¨
£¨
![]() °◊
°◊![]() ,
,
![]() £¨
£¨ ![]() °’
°’![]() ,
, ![]()
°ŗ![]() °◊
°◊![]() ,
,
°ŗ![]() ,
,
°ŗ![]() °◊
°◊![]() ,
,
°ŗ![]() £¨
£¨
![]() ,
,
°ŗ![]() ;
;
Ęŕ¬ķ◊„£®ĽÚ![]() £©
£©
ņŪ”…»ÁŌ¬£ļ
°Ŗ![]() £¨
£¨ ![]()
°ŗ![]() «Ķ»ĪŖ»żĹ«–ő£¨
«Ķ»ĪŖ»żĹ«–ő£¨
°ŗ![]() £¨
£¨ ![]()
”÷°Ŗ![]() £¨
£¨
°ŗ![]()
°ŗ![]() «Ķ»ĪŖ»żĹ«–ő
«Ķ»ĪŖ»żĹ«–ő
![]() £¨
£¨ ![]() °’
°’![]() £¨
£¨ ![]() £¨
£¨
°ŗ![]()
‘ŕ![]() ļÕ
ļÕ![]() ÷–£¨
÷–£¨ 
°ŗ![]() °’
°’![]()
°ŗ![]()
°ŗ![]()
°ŗ![]()
£®2£©¬ķ◊„£®ĽÚ![]() £©
£©
ņŪ”…»ÁŌ¬£ļ ![]()
ĘŔ![]() °Ŗ
°Ŗ![]() °ŗ
°ŗ![]() °◊
°◊![]()
°ŗ![]() °◊
°◊![]() °ŗ
°ŗ![]()
”…£®2£©÷™![]()
°ŗ![]() °◊
°◊![]() °ŗ
°ŗ![]()
”÷°Ŗ![]() °ŗ
°ŗ![]()
°ŗ![]() °ŗ
°ŗ![]()
īň Ī£¨ ![]() £®ĽÚ
£®ĽÚ![]() £©
£©
ĘŕĶĪ![]() £¨Õ¨ņŪŅ…÷§
£¨Õ¨ņŪŅ…÷§![]() īň Ī
īň Ī![]()
◊Ř…Ōňý Ų£ļĶĪ![]() Ī£¨
Ī£¨ ![]()
ĶĪ![]() Ī£¨
Ī£¨
![]() £®ĽÚ
£®ĽÚ![]() £©
£©