Question

【题目】今年我国多个省市遭受严重干旱，受旱灾的影响，4月份，我市某蔬菜价格呈上升趋势，其前四周每周的平均销售价格变化如表：

周数x	1	2	3	4
价格y（元/千克）	2	2.2	2.4	2.6

（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式；

（2）进入5月，由于本地蔬菜的上市，此种蔬菜的平均销售价格y（元/千克）从5月第1周的2.8元/千克下降至第2周的2.4元/千克，且y与周数x的变化情况满足二次函数y＝﹣x2+bx+c，请求出5月份y与x的函数关系式；

（3）若4月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m＝x+1.2，5月份此种蔬菜的进价m（元/千克）与周数x所满足的函数关系为m＝﹣x+2．试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大？且最大利润分别是多少？

Answer 1

【答案】（1）y＝0.2x+1.8；（2）y＝ x2x+3.1；（3）应在第一周的利润最大，1（元/千克）．

【解析】

（1）从表格看出，x每增加1，y就增加0.2，由此可确定是一次函数关系式，继而代入两点可得出解析式;

（2）把x=1，y=2.8和x=2，y=2.4，分别代入y＝﹣x2+bx+c，可求b，c的值,确定二次函数解析式;

（3）根据一次函数，二次函数的性质及自变量的取值范围,求最大利润.

解：（1）通过观察可见四月份周数y与x 的符合一次函数关系式，设这个关系式为：y＝kx+b，

则，

解得：，

∴4月份y与x 的函数关系式为y＝0.2x+1.8；

（2）将（1，2.8）（2，2.4）代入y＝﹣x2+bx+c．

可得：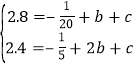

解之：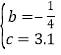

即x2

（3）4月份此种蔬菜利润可表示为：W1＝y﹣m＝（0.2x+1.8）﹣（x+1.2），即：W1＝﹣0.05x+0.6；

由函数解析式可知，四月份的利润随周数的增大而减小，所以应在第一周的利润最大，最大为：W＝﹣0.05×1+0.6＝0.55（元/千克），

5月份此种蔬菜利润可表示为：W2＝y﹣m＝（x2x+3.1）﹣（﹣x+2），

即：W2＝x2﹣x+1.1

由函数解析式可知，五月份的利润随周数变化符合二次函数且对称轴为：x＝﹣＝﹣，

即在第1至4周的利润随周数的增大而减小，所以应在第一周的利润最大，最大为：W＝﹣+1.1＝1（元/千克）．