题目内容
【题目】已知甲沿周长为300米的环形跑道上按逆时针方向跑步，速度为a米/秒，与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步，速度为3米/秒.设运动时间为t秒.
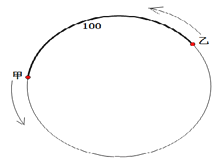
(1)若a=5，求甲、乙两人第1次相遇的时间；
(2)当t=50时，甲、乙两人第1次相遇.
①求a的值；
②若
时，甲、乙两人第1次相遇前，当两人相距120米时，求
的值.
【答案】（1）t=100（2）① a=1或7 ②t=5或20
【解析】
（1）根据相遇时，甲和乙的路程差等于200米,列方程即可求解；
（2）①由第1次相遇时间为50秒，分两种情况：当
时,乙和甲的路程差等于100米；当
时甲和乙的路程差等于200米列方程即可求出a值；
②当时由①可知a=7，分两种情况讨论：一种是乙距甲120米，即在100米的基础上甲又比乙多跑20米，此时两人在第一次相遇前相距120米，另一种是甲距乙120米，即在200米的基础上甲又比乙多跑80米，此时两人在第一次相遇前相距120米，即可得出t值.
（1）由题可列方程
，
解得：
，
答：若
=5,甲、乙两人第1次相遇的时间为100秒.
（2）①有两种情况：
当时，则
，解得
，
当时，则
，解得
，
所以a=1或7；
②当时由①可知a=7，根据题意可列方程：
，或
解得，t=5或20.
练习册系列答案
相关题目
