Question

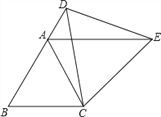
【题目】如图，△ABC为等边三角形，D为边BA延长线上一点，连接CD，以CD为一边作等边△CDE，连接AE．

（1）求证：△CBD≌△CAE；

（2）求证：AE∥BC．

Answer 1

【答案】（1）证明见解析；（2）AE∥BC．理由见解析.

【解析】试题分析：（1）只要证明∠ACE=∠BCD，根据SAS即可证明．

（2）只要证明∠CAE=∠ACB=60°即可．

试题解析：（1）证明：∵△ABC，△DCE为等边三角形，∴AC=BC，EC=DC，∠ACB=∠ECD=∠B=60°，∴∠ACE=∠BCD，在∠ACE和△BCD中，∵AC=BC，∠ACE=∠BCD，EC=DC，∴△ACE≌△BCD（SAS）；

（2）证明：∵△ACE≌△BCD，∴∠EAC=∠DBC=60°，∵∠ACB=∠DBC=60°，∴∠EAC=∠ACB=60°，∴AE∥BC．