题目内容
在直角坐标系中，已知A（3，3），在x轴、y轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P共有
- A.4个
- B.6个
- C.8个
- D.10个
C
分析：作出图形，以AO为底边与腰长两种情况确定出点P的位置，即可得解．
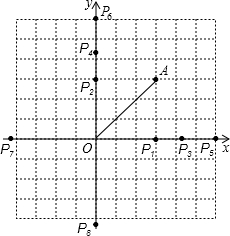
解答：如图所示，AO为底边时，点P可以有两个位置，
AO为腰长时，点P可以有6个位置，
所以，符合条件的点P共有8个．
故选C．
点评：本题考查了等腰三角形的判定，坐标与图形性质，熟练掌握等腰三角形的判定方法，作出图形更形象直观．
分析：作出图形，以AO为底边与腰长两种情况确定出点P的位置，即可得解．
解答：如图所示，AO为底边时，点P可以有两个位置，
AO为腰长时，点P可以有6个位置，
所以，符合条件的点P共有8个．
故选C．
点评：本题考查了等腰三角形的判定，坐标与图形性质，熟练掌握等腰三角形的判定方法，作出图形更形象直观．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
如图，在直角坐标系中，已知直线y=kx+6与x轴、y轴分别交于A、B两点，且△ABO的面积为12．
的直角顶点的坐标为