题目内容
.如图13,D为 O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是 O的切线;
O的切线;
(2)过点B作 O的切线交CD的延长线于点E,若BC=6,tan∠CDA=
O的切线交CD的延长线于点E,若BC=6,tan∠CDA= ,求BE的长
,求BE的长
 O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)求证:CD是
 O的切线;
O的切线;(2)过点B作
 O的切线交CD的延长线于点E,若BC=6,tan∠CDA=
O的切线交CD的延长线于点E,若BC=6,tan∠CDA= ,求BE的长
,求BE的长
(1)证明:连OD,OE,如图,

∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,
∴ED=EB,O D⊥BD,
D⊥BD,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA= ,
,
∴tan∠OEB= ,
,
∵Rt△CDO∽Rt△CBE,
∴ ,
,
∴CD= ,
,
在Rt△CBE中,设BE= ,
,
∴ ,
,
解得 .
.
即BE的长为 .
.

∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,
∴ED=EB,O
 D⊥BD,
D⊥BD,∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA=
 ,
,∴tan∠OEB=
 ,
,∵Rt△CDO∽Rt△CBE,
∴
 ,
,∴CD=
 ,
,在Rt△CBE中,设BE=
 ,
,∴
 ,
,解得
 .
.即BE的长为
 .
.略

练习册系列答案
相关题目

 果⊙O的半径是6cm,EC=8cm,求GF的长.
果⊙O的半径是6cm,EC=8cm,求GF的长.
 D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F .
D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F . 
 B.
B. -4
-4
 ⊙O与Rt△ABC的边AB相切于点X,与边CB相切于点Y.请你在图2中作出并标明⊙O的圆心O;(用尺规作图,保留作图痕迹,不写作法和证明)
⊙O与Rt△ABC的边AB相切于点X,与边CB相切于点Y.请你在图2中作出并标明⊙O的圆心O;(用尺规作图,保留作图痕迹,不写作法和证明) 求出s的最大值;若不能,请你说明不能确定s的最大值的理由.
求出s的最大值;若不能,请你说明不能确定s的最大值的理由.
 中,以点(-3,4)为圆心,4为半径的圆
中,以点(-3,4)为圆心,4为半径的圆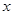 轴相交,与
轴相交,与 轴相切
轴相切 ,CA=CB,CD∥AB且与OA的延长线交与点D.
,CA=CB,CD∥AB且与OA的延长线交与点D.