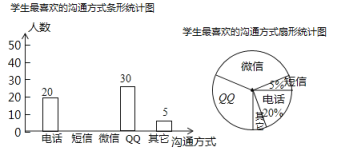
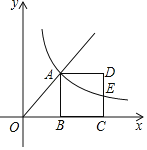
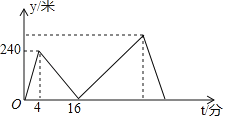
题目内容
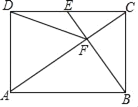
【题目】如图,在![]() 中,点
中,点![]() 是对角线
是对角线![]() ,
,![]() 的交点,
的交点,![]() ,
,![]() .点
.点![]() 为线段
为线段![]() 上一点,且满足
上一点,且满足![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
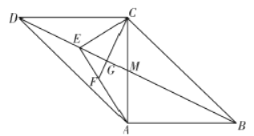
(1)若![]() ,求
,求![]() ;
;
(2)求证:![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)先求出CM和DC的长,然后运用勾股定理求得DM,最后运用等面积法即可解答;
(2)先证![]() ,再利用全等三角形的性质和等量代换即可证明.
,再利用全等三角形的性质和等量代换即可证明.
(1)![]() 四边形
四边形![]() 是平行四边形,点
是平行四边形,点![]() 是对角线
是对角线![]() ,
,![]() 的交点,
的交点,
![]() .
.
![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,![]()
![]() .
.
![]() ,
,
![]() 在
在![]() 中,
中,![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]() ,
,
![]()
(2)证明:∵AE⊥CE,AC⊥CD
∴∠AEC=90°,∠ACD=90°
∴∠EAC+∠ACE=90°,∠DCE+∠ACE=90°
∴∠EAC=∠DCE
同理:∠ACF=∠CDE
在△ACF和△CDE中
∠ACF=∠CDE,AC=CD,∠FAC=∠ECD
∴△ACF≌△CDE
∴CF=DE
∴DM=DE+EM,DM=CF+EM,BM=DM
∴CF+EM=BM

练习册系列答案
相关题目