题目内容
在实数范围内解下列方程:(1)x4+x3+x+1=0;(2)| x+8 |
| 2-x |
分析:(1)运用因式分解法解方程;(2)先将常数项5移到等号右边,然后两边平方,将无理方程转化为有理方程求解.
解答:解:(1)x4+x3+x+1=0
(x+1)x3+x+1=0
(x+1)(x3+1)=0
(x+1)2(x2-x+1)=0
则x+1=0,x=-1.
∴原方程的解为x=-1.
(2)
+
-5=0
+
=5
x+8+2-x+2
=25
2
=15
x2+6x+
=0
∵△=36-161=-125<0,
∴原方程无解.
(x+1)x3+x+1=0
(x+1)(x3+1)=0
(x+1)2(x2-x+1)=0
则x+1=0,x=-1.
∴原方程的解为x=-1.
(2)
| x+8 |
| 2-x |
| x+8 |
| 2-x |
x+8+2-x+2
| (x+8)(2-x) |
2
| (x+8)(2-x) |
x2+6x+
| 161 |
| 4 |
∵△=36-161=-125<0,
∴原方程无解.
点评:(1)在将一个四项式分解因式时,应用分组分解法,这里是等项分组,还用到了立方和公式:a3+b3=(a+b)(a2-ab+b2).
(2)解无理方程的基本思想是通过两边平方,将无理方程转化为有理方程,因此,解无理方程一定要检验.
(2)解无理方程的基本思想是通过两边平方,将无理方程转化为有理方程,因此,解无理方程一定要检验.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
 +
+ -5=0.
-5=0. +
+ -5=0.
-5=0.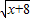 +
+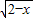 -5=0.
-5=0.