题目内容
若一个三角形的两个内角的平分线所成的钝角为145°，则这个三角形的形状为（ ）
| A、锐角三角形 | B、直角三角形 | C、钝角三角形 | D、等腰三角形 |
分析：如图，CD，BD分别是∠ACB，∠ABC的角的平分线，∠D=145°．要判断△ABC的形状，需算出△ABC中内角的度数．
解答：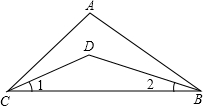
解：如图，CD，BD分别是∠ACB，∠ABC的角的平分线，∠D=145°．
在△BCD中，∠1+∠2+∠D=180°，
∴∠1+∠2=180°-145°=35°．
∵∠1=
∠ACB，∠2=
∠ABC，
∴∠ACB+∠ABC=2（∠1+∠2）=70°，
∴∠A=180°-（∠ACB+∠ABC）=110°，
∴△ABC的形状为钝角三角形．
故选C．
解：如图，CD，BD分别是∠ACB，∠ABC的角的平分线，∠D=145°．在△BCD中，∠1+∠2+∠D=180°，
∴∠1+∠2=180°-145°=35°．
∵∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ACB+∠ABC=2（∠1+∠2）=70°，
∴∠A=180°-（∠ACB+∠ABC）=110°，
∴△ABC的形状为钝角三角形．
故选C．
点评：本题先根据三角形内角和定理求出∠1+∠2=35°，再根据角的平分线的性质求出∠ACB+∠ABC的值，再次利用三角形内角和定理求出∠A的度数，从而判断三角形的形状为钝角三角形．
练习册系列答案
阅读快车系列答案
相关题目
