题目内容
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.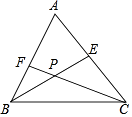
(1)若∠ABC=70°,∠ACB=50°,则∠BPC=°;
(2)求证:∠BPC=180°﹣ ![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数.
【答案】
(1)120
(2)解:证明:∵∠ABC和∠ACB的平分线BE、CF相交于点P,
∴∠PBC= ![]() ∠ABC,∠PCB=
∠ABC,∠PCB= ![]() ∠ACB,
∠ACB,
∵∠BPC+∠PBC+∠PCB=180°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣( ![]() ∠ABC+
∠ABC+ ![]() ∠ACB)=180°﹣
∠ACB)=180°﹣ ![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∴∠BPC=180°﹣ ![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
(3)解:解:在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∵由(2)可知:∠BPC=180°﹣ ![]() ∠ABC+∠ACB),
∠ABC+∠ACB),
∴∠BPC=180°﹣ ![]() (180°﹣∠A),
(180°﹣∠A),
∵∠A=α,
∴∠BPC=180°= ![]() (180°﹣α)=90°+
(180°﹣α)=90°+ ![]()
【解析】
①根据已知条件求出∠ABC+∠ACB,再根据角平分线的定义求出∠BPC+∠PCB,然后利用三角形的内角和等于180°列出计算.
②根据三角形的内角和和角平分线的定义即可得出结论.
③根据三角形的内角和和角平分线的定义即可.
【考点精析】根据题目的已知条件,利用三角形的内角和外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目