题目内容

若一个多边形的每个外角都为36°，则这个多边形的对角线共有
 
条．
考点：多边形内角与外角,多边形的对角线
专题：
分析：用360°除以每一个外角的度数求出边数，再根据多边形的对角线公式
n(n-3)
2
计算即可得解．
解答：解：多边形的边数=360°÷36°=10，
对角线条数=
10×(10-3)
2
=35条．
故答案为：35．
点评：本题考查了多边形的内角和外角，多边形的对角线，熟记公式是解题的关键．
练习册系列答案
相关题目
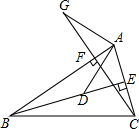如图，在△ABC中，BE，CF分别是边AC，AB上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD，AG，则AG与AD有何关系？试给出你的结论的理由．
如图，该图形围绕自己的旋转中心，至少旋转多少度能与自身重合的是（　　）
A、72°B、144°
C、180°D、360°
某公司6天内货品进出仓库的吨数如下：（“+”表示进库，“-”表示出库）
+20，-32，-17，+34，-38，-20
（1）经过这6天，仓库里的货品是
 
（填增多了还是减少了）
 
吨．
（2）经过这6天，仓库管理员结算发现仓库里还有货品460吨，那么6天前仓库里有货品多少吨？
（3）如果进出的装卸费都是每吨5元，那么这6天要付多少元装卸费．
读下列语句，并按照这些语句画出图形：
（1）在直线l上取三点A、B、C，在直线l外取一点P，画线段AP；画直线PC；画射线BP；
（2）射线OP的端点是直线m与直线n的交点，且点P不在直线m、n上；
（3）直线a、b相交于点C，直线b、c相交于点A，直线a、c相交于点B；
（4）在△ABC中，D、E分别是边AC、BC上的点，延长线段AB，反向延长线段ED相交于F．
在抗洪抢险中，人民解放军的冲锋船沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B地，约定向东为正方向，当天航行路程记录如下（单位：千米）
14，-9，18，-7，13，-6，10，-5
问：
（1）B地在A地何位置？
（2）若冲锋船每行驶1千米耗油0.5升，共耗油多少升油？
在同一个学校上学的小美、小泉、欧欧三位同学住在A、B、C三个住宅小区，如图所示，A、B、C三点共线，且AB=50米，BC=90米．他们打算合租一辆接送车上学（学校位于C的右边），由于车位紧张，准备在此之间只设一个停靠点，为使三位同学步行到停靠点的路程之和最小，你认为停靠点的位置应设在
 
．
画出数轴，在数轴上表示下列各数：-2，1.5，0，-3
1
2
，4，并按从小到大的顺序用“＜”连接上面各数．
若x1、x2是一元二次方程x2-3x+2=0的两根，则x1+x2和x1•x2的值分别是（　　）
A、3，-2B、3，2
C、-3，-2D、-3，2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网