题目内容
已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为
- A.y=x+2
- B.y=-x+2
- C.y=x+2或y=-x+2
- D.y=-x+2或y=x-2
C
分析:先求出一次函数y=kx+b与x轴和y轴的交点,再利用三角形的面积公式得到关于k的方程,解方程即可求出k的值.
解答:∵一次函数y=kx+b(k≠0)图象过点(0,2),
∴b=2,
令y=0,则x=- ,
,
∵函数图象与两坐标轴围成的三角形面积为2,
∴ ×2×|-
×2×|- |=2,即|
|=2,即| |=2,
|=2,
解得:k=±1,
则函数的解析式是y=x+2或y=-x+2.
故选C.
点评:本题考查一次函数图象上点的坐标特征和三角形的面积公式,有一定的综合性,注意点的坐标和线段长度的转化.
分析:先求出一次函数y=kx+b与x轴和y轴的交点,再利用三角形的面积公式得到关于k的方程,解方程即可求出k的值.
解答:∵一次函数y=kx+b(k≠0)图象过点(0,2),
∴b=2,
令y=0,则x=-
 ,
,∵函数图象与两坐标轴围成的三角形面积为2,
∴
 ×2×|-
×2×|- |=2,即|
|=2,即| |=2,
|=2,解得:k=±1,
则函数的解析式是y=x+2或y=-x+2.
故选C.
点评:本题考查一次函数图象上点的坐标特征和三角形的面积公式,有一定的综合性,注意点的坐标和线段长度的转化.

练习册系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.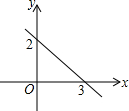 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.