Question

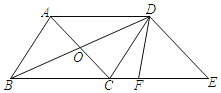
【题目】如图，在平行四边形ABCD中，对角线AC，BD交于点O，OA，OD满足等式+（OA-5）2=0，AD=13.

（1）求证：平行四边形ABCD是菱形；

（2）过点D作DE∥AC交BC的延长线于点E，DF平分∠BDE，请求出DF的长度．

Answer 1

【答案】（1）见解析；（2）DF=．

【解析】

（1）根据非负性得出OA=5，OD=12，利用勾股定理的逆定理得出AC⊥BD，利用菱形的判定解答；
（2）作辅助线，构建等腰直角三角形，则△FDG为等腰直角三角形，设FG=x，则BG=24-x，证明△BOC∽△BGF，可得x的值，从而得DF的长．

（1）∵+（OA-5）2=0，

∴OA=5，OD=12，

∴OA2+OD2=52+122=169，

∵AD=13，

∴AD2=169，

∴OA2+OD2=AD2，

∴∠AOD=90°，

∴AC⊥BD，

∴平行四边形ABCD是菱形；

（2）过F作FG⊥BD于G，

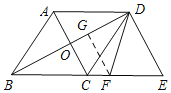
∵DE∥AC，AC⊥BD，

∴BD⊥DE，即∠BDE=90°，

∵DF平分∠BDE，

∴∠BDF=45°，

∴△FDG为等腰直角三角形，

∴DG=FG，

设FG=x，则BG=24-x，

∵OC∥FG，

∴△BOC∽△BGF，

∴，

∴，x=，

∴DF=FG=x=．