题目内容
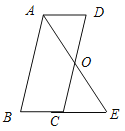
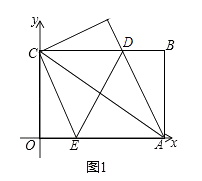
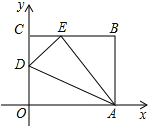
【题目】如图,四边形![]() 是一张放在平面直角坐标系中的长方形纸片,
是一张放在平面直角坐标系中的长方形纸片,![]() 为原点,点
为原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() .在
.在![]() 边上取一点
边上取一点![]() ,将纸片沿
,将纸片沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处.
处.
(1)求![]() 和
和![]() 的长;
的长;
(2)求直线![]() 的表达式;
的表达式;
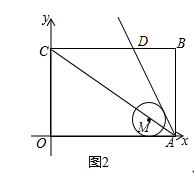
(3)直线![]() 与
与![]() 平行,当它与矩形
平行,当它与矩形![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根据勾股定理求出BE的长,进而可得出CE的长,在Rt△DCE中,由DE=OD及勾股定理可求出OD的长;
(2)根据CE、OD的长求得D、E的坐标,然后根据待定系数法即可求得表达式;
(3)根据平行的性质分析讨论即可求得.
解:(1)依题意可知,折痕![]() 是四边形
是四边形![]() 的对称轴,
的对称轴,
∴在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,解得
,解得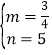 ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(3)∵直线![]() 与
与![]() 平行,
平行,
∴直线为![]() ,
,
∴当直线经过![]() 点时,
点时,![]() ,则
,则![]() ,
,
当直线经过![]() 点时,则
点时,则![]() ,
,
∴当直线![]() 与矩形
与矩形![]() 有公共点时,
有公共点时,![]() .
.
故答案为:(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目