题目内容
已知:如图,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.求证:四边形ABED是菱形.
【答案】分析:首先证明△BAE≌△DAE,可得BE=DE,再证明∠BAE=∠AEB,可得AB=BE,进而得到AB=BE=DE=AD,根据四条边都相等的四边形是菱形可以判定出四边形ABED是菱形.
解答:证明:∵AE平分∠BAD,
∴∠BAE=∠DAE,…(1分)
在△BAE和△DAE中,
∵ ,
,
∴△BAE≌△DAE(SAS)…(2分)
∴BE=DE,…(3分)
∵AD∥BC,
∴∠DAE=∠AEB,…(4分)
∴∠BAE=∠AEB,
∴AB=BE,…(5分)
∴AB=BE=DE=AD,…(6分)
∴四边形ABED是菱形.…(7分)
点评:此题主要考查了菱形的判定,关键是掌握菱形的判定方法:①菱形定义:一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形.③对角线互相垂直的平行四边形是菱形
解答:证明:∵AE平分∠BAD,
∴∠BAE=∠DAE,…(1分)
在△BAE和△DAE中,
∵
 ,
,∴△BAE≌△DAE(SAS)…(2分)
∴BE=DE,…(3分)

∵AD∥BC,
∴∠DAE=∠AEB,…(4分)
∴∠BAE=∠AEB,
∴AB=BE,…(5分)
∴AB=BE=DE=AD,…(6分)
∴四边形ABED是菱形.…(7分)
点评:此题主要考查了菱形的判定,关键是掌握菱形的判定方法:①菱形定义:一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形.③对角线互相垂直的平行四边形是菱形

练习册系列答案
相关题目
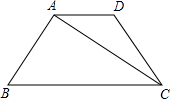 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.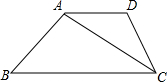 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,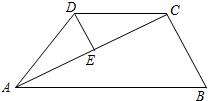 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=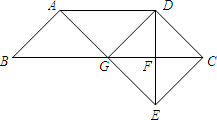 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.