题目内容
（2006•深圳）如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠ADC=120°．（1）求证：BD⊥DC；
（2）若AB=4，求梯形ABCD的面积．
【答案】分析：（1）根据已知条件发现等腰三角形，根据等腰三角形的性质以及等腰梯形的性质即可求解；
（2）根据（1）中的结论分析求得该梯形的高，即可求得面积．
解答：
（1）证明：∵AD∥BC，∠ADC=120°，
∴∠C=60°．
又∵AB=DC=AD，
∴∠ABC=∠C=60°，∠ABD=∠ADB=∠DBC=30°，
∴∠BDC=90°，BD⊥DC．
（2）解：过D作DE⊥BC于点E，
在Rt△DEC中，
∵∠C=60°，AB=DC=4，
∴
=sin∠C=sin60°，
∴DE=2
，
在Rt△BDC中，
=sin30°，BC=2DC=8，
∴S梯形=
（AD+BC）•DE=12
．
点评：考查等腰梯形的有关性质及综合推理能力．
（2）根据（1）中的结论分析求得该梯形的高，即可求得面积．
解答：
（1）证明：∵AD∥BC，∠ADC=120°，∴∠C=60°．
又∵AB=DC=AD，
∴∠ABC=∠C=60°，∠ABD=∠ADB=∠DBC=30°，
∴∠BDC=90°，BD⊥DC．
（2）解：过D作DE⊥BC于点E，
在Rt△DEC中，
∵∠C=60°，AB=DC=4，
∴
=sin∠C=sin60°，∴DE=2
，在Rt△BDC中，
=sin30°，BC=2DC=8，∴S梯形=
（AD+BC）•DE=12．点评：考查等腰梯形的有关性质及综合推理能力．
练习册系列答案
相关题目
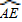的中点，AE交y轴于G点，若点A的坐标为（-2，0），AE=8．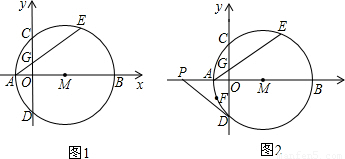
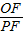的比值是否发生变化？若不变，求出比值；若变化，说明变化规律．
