��Ŀ����
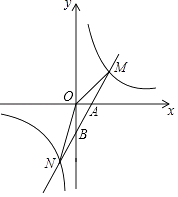
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A��BΪx�������㣬C��DΪy���ϵ����㣬������A��C��B�������ߵ�һ����C2��ϳ�һ��������ߣ����ǰ�����������߳�Ϊ�����ߡ�����֪��C������Ϊ��0���� ![]() ������M��������C2��y=mx2��2mx��3m��m��0���Ķ��㣮
������M��������C2��y=mx2��2mx��3m��m��0���Ķ��㣮
��1����A��B��������ꣻ
��2�������ߡ��ڵ����������Ƿ����һ��P��ʹ�á�PBC�������������ڣ������PBC��������ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��y=mx2��2mx��3m=m��x��3����x+1������m��0��
�൱y=0ʱ���ɵ�m��x��3����x+1��=0�����x1=��1��x2=3��
��A����1��0����B��3��0����
��2��
�⣺���A��B��C����������߽���ʽΪy=ax2+bx+c��
����  �����
�����  ��
��
��������C1����ʽΪy= ![]() x2��x��
x2��x�� ![]() ��
��
��ͼ������P��PQ��y�ᣬ��BC��Q��
��ֱ��BC����ʽΪy=kx+s������  �����
�����  ��
��
��ֱ��BC�Ľ���ʽΪy= ![]() x��
x�� ![]() ��
��
��P��x�� ![]() x2��x��
x2��x�� ![]() ������Q��x��
������Q��x�� ![]() x��
x�� ![]() ����
����
��PQ= ![]() x��
x�� ![]() ����
���� ![]() x2��x��
x2��x�� ![]() ��=��
��=�� ![]() x2+
x2+ ![]() x��
x��
��S��PBC= ![]() PQOB=
PQOB= ![]() ������
������ ![]() x2+
x2+ ![]() x����3=��
x����3=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
�൱x= ![]() ʱ��S��PBC�����ֵ��S���=
ʱ��S��PBC�����ֵ��S���= ![]() ��
��
![]() ����
���� ![]() ��2��
��2�� ![]() ��
�� ![]() =��
=�� ![]() ����ʱP������Ϊ��
����ʱP������Ϊ�� ![]() ����
���� ![]() ����
����

����������1���������߽�����������y=0�����x��ֵ��������A��B�����ꣻ��2����A��B��C�����꣬����þ�����A��B��C�������߽���ʽ������BC������P��PQ��y�ᣬ��BC�ڵ�Q����B��C����������ֱ��BC�Ľ���ʽ��������P�����꣬�Ӷ���ʾ��Q�����꣬������PQ�ij����Ӷ���P�������ʾ����PBC����������ö��κ��������ʿ����P������͡�PBC��������ֵ��
�����㾫�������ն��κ�����ͼ��Ͷ��κ����������ǽ����ĸ�������Ҫ֪�����κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�