Question

16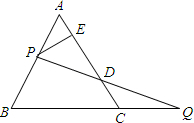．如图，过边长为4的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为2．

Answer 1

分析 过P作PF∥BC交AC于F，得出等边三角形APF，推出AP=PF=QC，根据等腰三角形性质求出EF=AE，证△PFD≌△QCD，推出FD=CD，推出DE=$\frac{1}{2}$AC即可．

解答 解：过P作PF∥BC交AC于F．
∵PF∥BC，△ABC是等边三角形，
∴∠PFD=∠QCD，△APF是等边三角形，
∴AP=PF=AF，
∵PE⊥AC，
∴AE=EF，
∵AP=PF，AP=CQ，
∴PF=CQ．
∵在△PFD和△QCD中，
$\left\{\begin{array}{l}{∠PFD=∠QCD}\\{∠PDF=∠QDC}\\{PF=CQ}\end{array}\right.$，
∴△PFD≌△QCD（AAS），
∴FD=CD，
∵AE=EF，
∴EF+FD=AE+CD，
∴AE+CD=DE=$\frac{1}{2}$AC，
∵AC=4，
∴DE=$\frac{1}{2}×4=2$．
故答案为：2．

点评 本题考查了全等三角形的性质和判定，等边三角形的性质和判定，等腰三角形的性质，平行线的性质等知识点的应用，能综合运用性质进行推理是解此题的关键，通过做此题培养了学生分析问题和解决问题的能力，题型较好，难度适中．