题目内容
已知x=-1是方程x2+mx-5=0的一个根，则m= ，方程的另一根为 ．
【答案】分析：把x=-1代入原方程，即可求m，再把m的值代入，可得关于x的一元二次方程，利用因式分解法求解方程，可得x1=5，x2=-1，从而可求答案．
解答：解：把x=-1代入方程，得（-1）2-m-5=0，
∴m=1-5=-4，
∴原方程为x2-4x-5=0，
∴（x-5）（x+1）=0，
解得x1=5，x2=-1，
即另一根为x=5．
故答案是-4；x=5．
点评：本题考查了一元二次方程的解，解题的关键是理解方程的根的概念以及使用因式分解法解方程．
解答：解：把x=-1代入方程，得（-1）2-m-5=0，
∴m=1-5=-4，
∴原方程为x2-4x-5=0，
∴（x-5）（x+1）=0，
解得x1=5，x2=-1，
即另一根为x=5．
故答案是-4；x=5．
点评：本题考查了一元二次方程的解，解题的关键是理解方程的根的概念以及使用因式分解法解方程．
练习册系列答案
相关题目
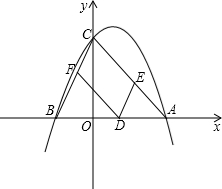如图所示，已知实数m是方程x2-8x+16=0的一个实数根，抛物线y=