题目内容
已知m、n是等腰三角形的两条边,且m、n满足| m-8 |
分析:由已知等式,结合非负数的性质求m、n的值,再根据m、n分别作为等腰三角形的腰,分类求解.
解答:解:∵
+(n-6)2=0,
∴m-8=0,n-6=0,
解得m=8,n=6,
当m=8作腰时,三边为8,8,6,符合三边关系定理,周长为:8+8+6=22,
当m=6作腰时,三边为8,6,6,符合三边关系定理,周长为:8+6+6=20.
故答案为:22或20.
| m-8 |
∴m-8=0,n-6=0,
解得m=8,n=6,
当m=8作腰时,三边为8,8,6,符合三边关系定理,周长为:8+8+6=22,
当m=6作腰时,三边为8,6,6,符合三边关系定理,周长为:8+6+6=20.
故答案为:22或20.
点评:本题考查了等腰三角形的性质,非负数的性质.关键是根据非负数的性质求m、n的值,再根据m或n作为腰,分类求解.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 互唯一确定的.
互唯一确定的.
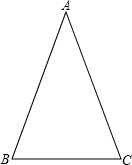
 中,AB=AC=x,BC=6,则腰长x的取值范围是3<x<6;④要了解一批灯管的使用寿命,从中选取了20只进行测试,在这个问题中20支灯管是样本容量;⑤已知
中,AB=AC=x,BC=6,则腰长x的取值范围是3<x<6;④要了解一批灯管的使用寿命,从中选取了20只进行测试,在这个问题中20支灯管是样本容量;⑤已知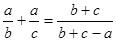 ,则
,则 有下面4个结论:
有下面4个结论: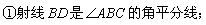 ②
②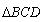 是等腰三角
是等腰三角
