题目内容
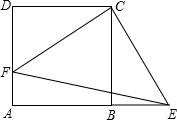
如图,在正方形ABCD中,AB=1,E、F分别是BC、CD边上点,若CE=
CB,CF=
CD,则图中阴影部分的面积是______.

| 1 |
| 2 |
| 1 |
| 2 |

延长GE到M,使GE=EM,连接CG、CM、BM,过C作CN⊥DE于N,
∵E为BC中点,
∴BE=EC=
| 1 |
| 2 |
在△BEG和△CEM中
|
∴△BEG≌△CEM(SAS),
∴S△BEG=S△CEM,
∵E、F分别为BC、CD中点,
∴DG:EG=2:1,
∴GM=DG=2EG,
∴S△MGC=S△DGC,
∴S△DMC=2S△DGC=2×
| 2 |
| 3 |
∵S△DEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴S△DMC=
| 1 |
| 3 |
∴阴影部分的面积S=S正方形ABCD-S△DMC=1×1-
| 1 |
| 3 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |


练习册系列答案
相关题目