题目内容
【题目】今年9月8日,重庆首家海底捞在来福士广场正式开始试营业,由于重庆人偏好麻辣口味,海底捞来福士店在原有番茄、红汤牛油、菌菇等多种常规锅底的基础上,专门为重庆人私人订制了一种“双椒锅底”.开业当天,人气爆满,番茄锅和双椒锅成为最受欢迎的两种锅底,总计销售300份,销售总额为9800元.其中双椒锅的销售单价是42元,番茄锅的销售单价为28元.
(1)求开业当天番茄锅销售数量;
(2)试营业一段时间后,商家发现番茄锅和双椒锅的日均销量之比为3:2.为了庆祝国庆,回馈广大顾客,海底捞在国庆期间推出了优惠活动,在原有售价的基础上将番茄锅降价![]() a%,双椒锅降价a%进行销售.10月1日当天,番茄锅的销量比日均销量增加了a%,而双椒锅的销量比日均销量增加了2a%,结果当天这两种锅底的销售总额比日均销售总额多了
a%,双椒锅降价a%进行销售.10月1日当天,番茄锅的销量比日均销量增加了a%,而双椒锅的销量比日均销量增加了2a%,结果当天这两种锅底的销售总额比日均销售总额多了![]() a%,求a的值.
a%,求a的值.
【答案】(1)200份;(2)40
【解析】
(1)设开业当天番茄锅销售数量为x份,则双椒锅的销售数量为(300﹣x)份,由题意得关于x的一元一次方程,求解即可;
(2)由番茄锅和双椒锅的日均销量之比为3:2,设番茄锅和双椒锅的日均销量分别为3m和2m,根据实行优惠后的销售总额等于原来销售总额的(1+![]() ),列方程,再设a%=t,解关于t的方程,解出t,则可得a的值.
),列方程,再设a%=t,解关于t的方程,解出t,则可得a的值.
解:(1)设开业当天番茄锅销售数量为x份,则双椒锅的销售数量为(300﹣x)份,由题意得:
28x+42(300﹣x)=9800,
解得:x=200;
∴开业当天番茄锅销售数量为200份.
(2)∵番茄锅和双椒锅的日均销量之比为3:2
∴设番茄锅和双椒锅的日均销量分别为3m和2m
根据题意得:28(1﹣![]() a%)×3m(1+a%)+42(1﹣a%)×2m×(1+2a%)=(28×3m+42×2m)×(1+
a%)×3m(1+a%)+42(1﹣a%)×2m×(1+2a%)=(28×3m+42×2m)×(1+![]() a%)
a%)
化简得:(1﹣![]() a%)(1+a%)+(1﹣a%)(1+2a%)=2(1+
a%)(1+a%)+(1﹣a%)(1+2a%)=2(1+![]() a%)
a%)
设a%=t,则有:
(1﹣![]() t)(1+t)+(1﹣t)(1+2t)=2(1+
t)(1+t)+(1﹣t)(1+2t)=2(1+![]() t),
t),
∴1+t﹣![]() ﹣
﹣![]() +1+2t﹣t﹣2t2=2+
+1+2t﹣t﹣2t2=2+![]() ,
,
∴t﹣![]() =0
=0
∴t=0(舍)或t=40%
∴a=40.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】为了了解某小区青年对“高铁”、“扫码支付”、“网购”和“共享单车”新四大发明的喜爱程度,随机调查该小区一部分青年(每名青年只能选一个),并将调查结果制成如图所示统计表与条形统计图.
青年最喜爱的新四大发明人数统计表
节目 | 人数(名) | 百分比 |
共享单车 | 5 |
|
扫码支付 | 15 |
|
网购 |
|
|
高铁 | 10 |
|
青年最喜爱的新四大发明人数条形统计图
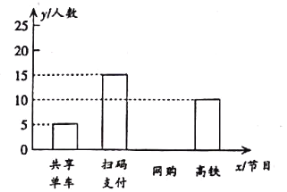
(1)计算![]() 的值
的值![]() ;
;
(2)请补全条形统计图;
(3)在被调查喜爱“共享单车”青年中,小明一周内使用共享单车的次数分别为:1,3,5,12,![]() ,若整数
,若整数![]() 是这组数据的中位数,直接写出该组数据的平均数.
是这组数据的中位数,直接写出该组数据的平均数.