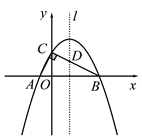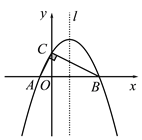题目内容
【题目】在等边![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上.
上.
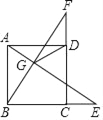
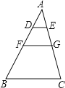
(1)如图![]() ,若
,若![]() ,以
,以![]() 为边作等边
为边作等边![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
求证:①![]() ;
;
②![]() 平分
平分![]() .
.
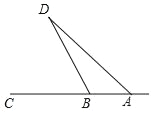
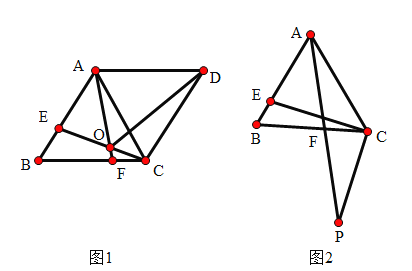
(2)如图![]() ,若
,若![]() ,作
,作![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() .
.
【答案】(1)①见解析;②见解析;(2)见解析
【解析】
(1)①利用SAS即可证出△ABF≌△CAE,再根据全等三角形的性质即可证出结论;
②过点D作DM⊥AF于M,作DN⊥EC交EC延长线于N,利用AAS证出△ADM≌△CDN,即可得出DM=DN,然后根据角平分线的判定定理即可证出结论;
(2)在CB上截取一点G,使CF=FG,连接AG,利用SAS证出△EAC≌△GCA,可得CE=AG,∠AEC=∠CGA,然后利用ASA证出△AGF≌△PCF,可得AG=CP,从而证出结论.
解:(1)①△ABC为等边三角形
∴AB=CA,∠B=∠CAE=∠BAC=60°
在△ABF和△CAE中
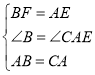
∴△ABF≌△CAE
∴![]()
②过点D作DM⊥AF于M,作DN⊥EC交EC延长线于N
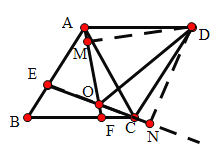
∵△ABF≌△CAE
∴∠BAF=∠ACE
∴∠AOC=180°-∠ACE-∠OAC=180°-∠BAF-∠OAC=180°-∠BAC=120°
∴∠MDN=360°-∠AOC-∠DMO-∠DNO=60°
∵△ACD为等边三角形
∴DA=DC,∠ADC=60°
∴∠ADC=∠MDN
∴∠ADC-∠MDC=∠MDN-∠MDC
∴∠ADM=∠CDN
在△ADM和△CDN中
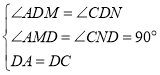
∴△ADM≌△CDN
∴DM=DN
∴![]() 平分
平分![]()
(2)在CB上截取一点G,使CF=FG,连接AG
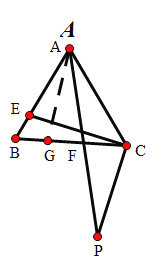
∵AE=2CF,CG=CF+FG=2CF
∴AE=CG
∵△ABC为等边三角形
∴∠EAC=∠GCA=60°
在△EAC和△GCA中
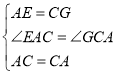
∴△EAC≌△GCA
∴CE=AG,∠AEC=∠CGA
∵∠AEC=∠BCP
∴∠CGA=∠BCP,即∠AGF=∠PCF
在△AGF和△PCF中
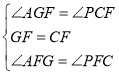
∴△AGF≌△PCF
∴AG=CP
∴CE=CP

 名校课堂系列答案
名校课堂系列答案