Question

（2013•武汉）如图，⊙A与⊙B外切于点D，PC，PD，PE分别是圆的切线，C，D，E是切点．若∠CDE=x°，∠ECD=y°，⊙B的半径为R，则

DE

的长度是（　　）

• A．

  π(90-x)R

  90

• B．

  π(90-y)R

  90

• C．

  π(180-x)R

  180

• D．

  π(180-y)R

  180

Answer 1

分析：点C、D、E都在⊙P上，由圆周角定理可得：∠DPE=2y°；然后在四边形BDPE中，求出∠B；最后利用弧长公式计算出结果．

解答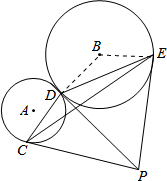：解：根据题意，由切线长定理可知：PC=PD=PE，
即点C、D、E在以P为圆心，PC长为半径的⊙P上，
由圆周角定理得：∠DPE=2∠ECD=2y°．
如图，连接BD、BE，则∠BDP=∠BEP=90°，
在四边形BDPE中，∠B+∠BDP+∠DPE+∠BEP=360°，
即：∠B+90°+2y°+90°=360°，
解得：∠B=180°-2y°．
∴

DE

的长度是：

(180-2y)πR

180

=

π(90-y)R

90

．
故选B．

点评：本题考查圆的相关性质．解题关键是确定点C、D、E在⊙P上，从而由圆周角定理得到∠DPE=2∠ECD=2y°．