题目内容
如图①是一个长为2a,宽为2b的长方形纸片,其长方形的面积显然为4ab,现将此长方形纸片沿图中虚线剪开,分成4个小长方形,然后拼成如图②的一个正方形.
(1)图②中阴影正方形EFGH的边长为: _________________；
(2)观察图②,代数式(a -b)2表示哪个图形的面积？代数式(a+b)2呢？
(3)用两种不同方法表示图②中的阴影正方形EFGH的面积,并写出关于代数式(a+b)2、(a -b)2和4ab之间的等量关系；
(4)根据(3)题中的等量关系,解决如下问题:若a+b=7,ab=5,求:(a -b)2的值.
(1) a -b
(2) (a+b)2 :表示正方形ABCD的面积 (a -b)2 :表示正方形EFGH的面积(阴影部分)
(3) 方法1: 正方形EFGH的面积=(a-b)2 ； 方法2: 正方形EFGH的面积=正方形ABCD的面积-长方形的面积=(a+b)2-4ab ∴等量关系：(a -b)2=(a+b)2-4ab
(4) 29
解析试题分析： (1) 图②中阴影正方形EFGH的边长为:a-b
(2) (a+b)2 :表示正方形ABCD的面积 (a -b)2 :表示正方形EFGH的面积(阴影部分)
(3) 方法1: 正方形EFGH的面积=(a-b)2
方法2: 正方形EFGH的面积=正方形ABCD的面积-长方形的面积=(a+b)2-4ab
∴等量关系：(a -b)2=(a+b)2-4ab
(4)∵a+b=7,ab=5, ∴(a-b)2=72-4×5=29
考点：整式运算和几何综合运用
点评：本题难度中等，主要考查学生对整式运算和几何综合运用知识点的掌握。分析图像边长对应代数式为解题关键。
练习册系列答案
相关题目
24、如图1是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均匀分成四块小长方形，然后按图2形状拼成一个正方形．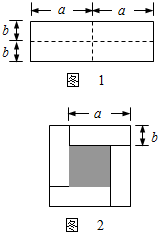
如图1是一个长为2a，宽为2b的长方形，沿图中虚线剪开分成四块小长方形，然后按如图2的形状拼成一个正方形．
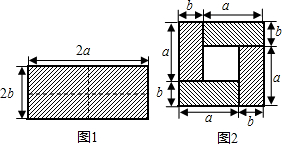四块小长方形，然后按图2形状拼成一个正方形．
