题目内容
若一个三角形的三边都是方程 的解,则此三角形的周长是_________.
的解,则此三角形的周长是_________.
【答案】
6或10或12.
【解析】
试题分析:求△ABC的周长,即是确定等腰三角形的腰与底的长求周长.首先求出方程的根,根据三角形三边关系定理列出不等式,然后解不等式即可.
解方程x2-6x+8=0得x1=4,x2=2;
当4为腰,2为底时,4-2<4<4+2,能构成等腰三角形,周长为4+2+4=10;
当2为腰,4为底时4-2≠<2<4+2不能构成三角形,
当等腰三角形的三边分别都为4,或者都为2时,构成等边三角形,周长分别为6,12,
故△ABC的周长是6或10或12.
考点:1解一元二次方程-因式分解法;2三角形三边关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 长,不必说明理由.
长,不必说明理由.
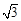 b,得a2-b2=(
b,得a2-b2=(